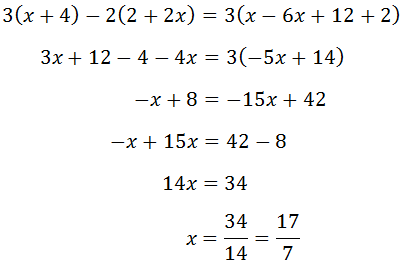Cuando la expresión algebraica cuenta con un solo término se denomina
monomio, si son dos, binomio, en el caso de tres, trinomio. Cuando
posee más de tres términos, se denomina polinomio, que en realidad es la
denominación que puede aplicarse siempre que exista más de un término.
Si la expresión algebraica no tiene denominador y las letras tienen
solamente potencias naturales, se dice que es entera; y fraccionaria en
caso contrario. Si bajo el signo radical, no tiene letras, se llama
racional, y si las tiene, se denomina irracional.
Dos expresiones algebraicas separadas por el signo de igualdad (=) se
llama ecuación, por ejemplo 4x+5 = 17. El valor que en este caso
satisface la incógnita, es 3, ese valor se conoce como solución o raíz.
La parte de la ecuación colocada antes, o sea, a la izquierda del signo
de igualdad, se denomina premier miembro, y lo que se escribe a la
derecha, segundo miembro.
terminos de expresiones alguebraicas
 ejemplos de expresiones alguebraicas
ejemplos de expresiones alguebraicas
Términos:
- 3a2b5 + 7y2 - abc6
- 6x2 + 98y3
2.- Monomios:
3.- Trinomios:
- 3n5y3 +23n5y8z3 – π2
- 3n - 22ª2 + 26n4
- xy + 18n3 - 2x2
4.- Polinomios (más de tres términos):
- 3n5y3 +23n5y8z3 – π2 3n - 22ª2 + 26n4
- xy + 18n3 - 2x2 - 9a3b4 - 19n291 +17xy+5k2
- 3a2b5 + 7y2 - abc6 + 6x2 + 98y3
ejemplos de axpresiones alguebraicas grado de minomios y polinomios
El exponente en 3x2 es 2
El exponente en 5x4 es 4
El exponente en -2 es 0, porque -2=-2x0 (x0=1)
Entonces
el grado de  es 4, el exponente de
mayor orden de la variable en el polinomio.
es 4, el exponente de
mayor orden de la variable en el polinomio.
De
manera semejante, el grado de  es 5, puesto que 5
es el exponente de mayor orden de una variable presente en el polinomio.
es 5, puesto que 5
es el exponente de mayor orden de una variable presente en el polinomio.
Por
convención, un número como -4 o 7 se conoce como polinomio de grado 0, porque
si a¹0,
a=ax°.
El
grado de un polinomio puede ser “absoluto” o “relativo” a una literal.
Grado absoluto: El
grado absoluto de un polinomio se determina por el exponente mayor, de uno de
sus términos.
 El
grado absoluto es cuatro.
El
grado absoluto es cuatro.
 El grado
absoluto es sexto.
El grado
absoluto es sexto.
 El grado
absoluto es quinto.
El grado
absoluto es quinto.
Grado relativo a una literal: El
grado relativo de un polinomio con respecto a una literal, es el mayor exponente
que tiene la literal que se considere del polinomio.
 El grado con relación a x es séptimo, de quinto grado con
relación a y.
El grado con relación a x es séptimo, de quinto grado con
relación a y.
 El
grado con relación a a es tres, de segundo grado con relación a b.
El
grado con relación a a es tres, de segundo grado con relación a b.
Polinomio cero
El
mismo número 0 se conoce como polinomio cero y no se le asigna grado. Se hace
notar que 0×x4=0,
0×x2=0,
0×x3=0,
y así sucesivamente de modo que los polinomios cero no pueden tener grado.
ejemplos de multiplicacion , division y restas de monomios
Sustracción de monomios
Para
restar monomios, se suma el minuendo con el sustraendo cambiado de
signo y se da el mismo proceso de la suma.
ejemplo: Sean los monomios
 y
y  su resta sería:
su resta sería:

Multiplicación de monomios
Para
multiplicar monomios, se suman los exponentes de cada variable, se
multiplican los números, y se juntan todas las variables.
Ejemplo: 


Multiplicación de fracciones
Para
multiplicar dos fracciones, unicamente es multiplicar el numerador de
la primera fracción con el numerador de la segunda fracción, y hacer lo
mismo con los denominadores.

Multiplicación de una fraccion con un número natural
Para
multiplicar una fracción con un número se multiplica el número con el
numerador, y el denominador por 1, ya que el número es una fracción con
denominador 1:

Multiplicación de dos fracciones
Para
multiplicar dos fracciones, se multiplican los denominadores y los
numeradores por los denominadores y los numeradores de las fracciones
restantes

Multiplicación de fracciones inversas
Cuando dos fracciones inversas se multiplican,
el resultado es la unidad.

Otras operaciones con fracciones
Potenciacion de fracciones
Hay
que decir que una potencia es aquella multiplicación donde se
multiplica la base por si misma tantas veces como lo indique el
exponente. Por lo que es una multiplicación de fracciones.

Radicación de fracciones
La
radicación es el proceso inverso a la potenciación. Para radicar una
fracción, se extrae la raiz enesíma al numerador y denominador.
![{\displaystyle {\sqrt[{3}]{\frac {8}{27}}}={\frac {\sqrt[{3}]{8}}{\sqrt[{3}]{27}}}={\frac {2}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bc1e4b0013f1cbef0e01ec7728a89c3dd0141b5)

Racionalización
En
el caso anterior, comprobamos que el denominador tenía una raiz
cuadrada en su denominador. Para evitar tal situacion, se debe
multiplicar la fracción con su
conjugada para hacer desaparecer la raiz en el denominador.

Existe el caso en el que el denominador tiene una suma de un número
entero con un radical. Para racionalizar, la conjugada debe completar
una diferencia de cuadrados.

acontinuacion video para mayor entendimiento
Cálculo del máimo común divisor y mínimo común múltiple
MÁXIMO COMÚN IVISOR:
El Máximo Común Divisor es, como su nombre indica, el mayor de los
divisores comunes de varios números. Para calcularlo, se descompone cada
uno de ellos en factores primos. El M.C.D. es el resultado de
multiplicar los factores que se repitan en todas las descomposiciones,
afectados por el menor exponente.
En el caso de que no se repita ningún factor, el M.C.D. de esos números
es 1, y se dice que los números son “primos entre sí”. Por ejemplo, el
18 y el 25 son primos entre sí.
Ejemplos:
Si queremos hallar el M.C.D. de 36, 60 y 72, descomponemos los tres en factores primos:
36 = 22·32
60 = 22·3·5
72 = 23·32
Vemos que los únicos factores que se repiten en las tres
descomposiciones son el 2 y el 3. Los cogemos con los menores exponentes
al que están afectados, por lo que el M.C.D. será 22·3 = 12.
M.C.D.(36, 60, 72) = 12
Para hallar el M.C.D. de 18 y 25:
18 = 2·32
25 = 52
No hay ningún factor repetido, luego:
M.C.D.(18, 25) = 1
Los números 18 y 25 son primos entre sí.
MÍNIMO COMÚN MÚLTIPLO:
El Mínimo Común Múltiplo es, así mismo, el menor de los múltiplos
comunes a varios números. Para calcularlo, descomponemos los números en
factores primos, y el M.C.M es el resultado de multiplicar los factores
comunes y los no comunes, afectados por el mayor exponente.
Si los números son primos entre sí, el M.C.M. es el producto entre ellos.
Ejemplos:
El M.C.M de 36, 60 y 72, que ya tenemos descompuestos más arriba. Los
factores que se repiten son el 2 y el 3, y los que no se repiten, el 5.
Los cogemos con los mayores exponentes, es decir, 23, 32 y 5. El M.C.M. es, por lo tanto:
M.C.M.(36, 60, 72) = 23·32·5 = 360
El M.C.M. de 18 y 25. Como no se repetía ningún factor, tenemos que
cogerlos todos, afectados con el exponente que llevan, es decir, estamos
cogiendo todos los factores, por lo que el M.C.M. es el producto de 18·25:
M.C.M.(18, 25) = 2·32·52 = 450
aqui veremos acontinuacion un video sobre lo planteado
opereraciones aritmeticas
Suma o adición
La suma es una operación que se deriva de la operación de
contar.
Si tenemos 6 ovejas y compramos 2 ovejas ¿cuantas ovejas
tenemos?. Una forma de hacerlo sería volver a contar todas las
ovejas, pero alguien que hubiese contado varias veces el mismo
caso, recordaria el resultado y no necesitaría volver a contar
las ovejas. Sabria que 6 + 2 = 8.
Los términos de la suma se llaman sumandos.
Propiedades de la suma:
a + b = b + a Esta propiedad se llama conmutativa.
Si tenemos que sumar varios numeros podemos hacerlo en
cualquier orden (esto se llama propiedad asociativa). Si
tenemos que sumar a, b, c y d, podemos sumar primero a + b,
despues c + d y despues sumar los dos resultados anteriores, o
podemos sumar a + c, despues b + d y despues sumar los dos
resultados anteriores o podemos sumar a + b y al resultado
sumarle c y al resultado sumarle d. En fin podemos sumar los
numeros en cualquier orden.
La suma tiene elemento neutro. El cero es el elemento
neutro de la suma porque siempre se cumple que a + 0 = a.
La suma tiene elemento simétrico. El elemento
simetrico de un número es otro que sumado al anterior da el
elemento neutro. El elemento simetrico de a es -a, porque a + (-a)
= 0
Resta o substración
Igual que la suma la resta es una operacion que se deriva de
la operacion de contar.
Si tenemos 6 ovejas y los lobos se comen 2 ovejas ¿cuantas
ovejas tenemos?. Una forma de hacerlo sería volver a contar
todas las ovejas, pero alguien que hubiese contado varias veces
el mismo caso, recordaria el resultado y no necesitaría volver a
contar las ovejas. Sabria que 6 - 2 = 4.
Los terminos de la resta se llaman minuendo (las
ovejas que tenemos) y sustraendo (las ovejas que se
comieron los lobos).
Propiedades de la resta:
La resta no tiene la propiedad conmutativa (no es lo mismo a -
b que b - a)
Producto o multiplicación
Muchas veces tenemos que sumar un número consigo mismo varias
veces. Por ejemplo, si tenemos que sumar 5 + 5 + 5 + 5 + 5 + 5 +
5, sería más breve representarlo asi 5 * 7 (esto significaria
sumar 5 condigo mismo 7 veces).
La multiplicación es una forma abreviada de hacer un tipo
especial de sumas.
Los terminos de la multiplicación se llaman multiplicando
(el numero que se suma) y multiplicador (el número de
veces que se suma).
Propiedades de la multiplicación
a * b = b * a. Esta propiedad se llama propiedad conmutativa
Si tenemos que multiplicar varios numeros podemos hacerlo en
cualquier orden (esto se llama propiedad asociativa). Si
tenemos que multiplicar a, b, c y d, podemos multiplicar primero
a . b, despues c . d y despues multiplicar los dos resultados
anteriores, o podemos multiplicar a . c, despues b . d y despues
multiplicar los dos resultados anteriores o podemos multiplicar a
. b y multiplicar el resultado por c y despues multiplicarlo por
d. En fin podemos multiplicar los numeros en cualquier orden.
La multiplicación tiene elemento neutro. El uno es
el elemento neutro de la multiplicación porque siempre se cumple
que a .1 = a.
La multiplicación tiene elemento simétrico. El
elemento simetrico de un número es otro que multiplicado por el
anterior da el elemento neutro. El elemento simetrico de a es 1/a,
porque a / a = 0
a(b + c) = a . c + a . d. Esta propiedad se llama distributiva
respecto a la suma.
División
La división es la operación que tenemos que hacer para
repartir un numero de cosas entre un número de personas.
Los terminos de la división se llaman dividendo (el
número de cosas), divisor (el número de personas), cociente
(el numero que le corresponde a cada persona) y resto (lo
que sobra).
Si el resto es cero la división se llama exacta y en caso
contrario inexacta.
Propiedades de la division
La divisón no tiene la propiedad conmutativa. No es lo mismo
a/b que b/a.
Potenciación
En bastantes ocasiones tenemos que multiplicar un número por
si mismo un número dado de veces.
Por ejemplo: 5 * 5 * 5 * 5 * 5 * 5 * 5
Una forma de representar esta operacion es 57 (esto
quiere decir que hay que multiplicar 5 por si mismo 7 veces).
El numero inferior se llama base y el superior exponente.
Propiedades de la potenciación:
am.an = am+n
am/an = am-n
a0 = 1 (se deriva de la propiedad anterior am/am
= 1 = am-m = a0)
(am)n = am.n
(a.b.c)m = am . bm .cm
a-n = 1/an (se deriva de la segunda
propiedad).
Radicación
La radicacion es la operacion inversa de la potenciación.
Supongamos que nos dan un número a y nos piden calcular otro,
tal que, multiplicado por si mismo un número b de veces nos da
el numero a.
Por ejemplo: calcular qué número multiplicado por si mismo 2
veces da 196. Ese número es 14.
El número que esta dentro de la raiz se llama radicando,
el grado de la raiz se llama índice del radical, el
resultado se llama raiz.
Podemos considerar la radicación como un caso particular de
la potenciación. En efecto, la raiz cuadrada de un numero (por
ejemplo a) es igual que a1/2, del mismo modo la raiz cúbica
de a es a1/3 y en general, la raiz enesima de un
numero a es a1/n.
La mejor forma de resolver los ejercicios de operaciones con
raices es convertir las raices a potencias y operar teneiendo en
cuenta las propiedades dadas para la operacion de potenciación.
representacion fraccionaria
Representación de números racionales en la recta numérica
Para representar los números racionales en la recta numérica, tienes que
comparar los números dados, para lo cual deberás transformar de número
decimal a fracción o de fracción a número decimal.
1.1- Representación de números decimales en la recta numérica
Si tienes que transformar las fracciones a número decimal, puedes ubicar
los números racionales en la recta numérica de la siguiente forma; si
son números negativos y positivos dibuja una recta dividida en 2 mitades
simétricas desde el origen, es decir, desde el número 0. A la izquierda
del número 0 ubicas los números negativos y a la derecha los números
positivos, de menor a mayor, manteniendo la misma distancia entre dos
números consecutivos. Para ubicar los décimos se divide la distancia
entre dos números consecutivos en 10 partes iguales. Los números
decimales inexactos los puedes aproximar para que sea más fácil
ubicarlos.
Una vez que ubiques todos los decimales en la recta numérica, puedes anotar los números racionales originales.
Recuerda que, los números positivos mientras más cerca
del cero menor será su valor y los números negativos mientras más cerca
del cero mayor será su valor.
Ejemplo: Representa los siguientes números racionales en la recta numérica;
- Primero debes transformar las fracciones a números decimales y el número mixto a fracción impropia y luego a número decimal.
| Recuerda: Para
transformar un número mixto a fracción impropia debes multiplicar el
entero por el denominador y sumar el numerador, este resultado se
escribe en el numerador y el denominador se mantiene igual. |
|
Ejemplo:
- Entonces los números que tienes que representar son los siguientes;

- Aproxima los números decimales inexactos, los que tienen centésimos
también los puedes aproximar. En este caso no aproximaremos, ya que,
sabemos que (0,05) se ubica en la mitad entre dos décimos de la recta
que dibujaremos.
- Ahora puedes comparar y ubicar los números decimales en la recta numérica.
- Anota los números racionales originales en la recta numérica.
razones y proporciones
Las razones y proporciones, nosotros denominamos
razón al cociente que es indicado por dos números y que representa la
relación entre dos cantidades y una proporción a la igualdad que existe
entre dos o más razones.
Razón. Una razón indica
en forma de división la relación entre dos cantidades. Nos indica
cuántas unidades hay en relación a las otras, y se suele indicar
simplificando las fracciones.
Por ejemplo, si en un salón de
clases tenemos 24 niñas y 18 niños, entonces lo representaremos de
alguna de las siguientes formas:
24/18
24:18
Y como la fracción podemos simplificarla al dividirla entre 6, entonces tendremos:
4/3
4:3
Y se lee que existe una razón de 4 a 3, o de 4 por cada 3.
Cada
uno de los valores de una razón tiene un nombre. El valor que está del
lado izquierdo de la relación, se le llama antecedente, y al valor del
lado derecho se le llama consecuente.
En este caso, la relación de niñas respecto a los niños es una relación de 4 a 3, o de 4 niñas por cada 3 niños.
Proporción.
La proporción indica mediante una igualdad la comparación de dos
razones. Para escribir una proporción, debemos tener en cuenta que los
valores antecedentes, siempre estén del mismo lado, al igual que los
consecuentes.
En nuestro ejemplo del salón de clases, podemos
comparar la razón que tenemos, de 4 niñas por cada 3 niños, y podremos
calcular cuántos niños hay en un salón en relación al número de niñas o
viceversa. Para esto, en primer lugar escribiremos la proporción que ya
conocemos:
4:3
Después, un signo de igualdad
4:3=
Y
después la cantidad total, por ejemplo la del mismo salón, recordando
que debemos respetar el orden del antecedente y del consecuente. En
nuestro ejemplo, el antecedente será el número de niñas, y el
consecuente el número de niños.
4:3=24:18
Para
comprobar la igualdad de la proporción, se efectúan dos
multiplicaciones. En una proporción, tomaremos como referencia el signo
de igualdad. Los números que están más cercanos, se llaman centros, y
los números más lejanos son los extremos. En nuestro ejemplo, los
números 3 y 24 son los más cercanos al signo igual, por lo que son los
centros. El 4 y el 18, son los extremos. Para comprobar que la
proporción es correcta, el producto de la multiplicación de los centros
debe ser igual al producto de la multiplicación de los extremos:
3 X 24 = 72
4 X 18 = 72
Proporción directa y proporción inversa:
Las proporciones pueden expresar relaciones en que el aumento de la
cantidad del antecedente aumenta la cantidad del consecuente. A esta
variación se le llama proporción directa. El ejemplo anterior es una
proporción directa.
En una proporción inversa, el aumento de la
cantidad en el antecedente, significa la disminución de la cantidad en
el consecuente.
Por ejemplo, en una mueblería, 6 trabajadores
hacen 8 sillones en 4 días. Si queremos saber cuántos trabajadores se
necesitan para construir los 8 sillones en 1, 2 y 3 días, usaremos una
proporción inversa.
Para determinarla, usaremos el número de trabajadores como cifra antecedente, y el número de días como cifra consecuente
:
6:4=
Siguiendo
el mismo orden, del otro lado de la igualdad tendremos como antecedente
nuevamente el número de trabajadores, y como consecuente los días que
tardarán. Tendremos algo como lo siguiente:
6:4 = ?:3
6:4 = ?:2
6:4 = ?:1
Para
determinar la proporción inversa, multiplicaremos los factores de la
razón conocida, en nuestro ejemplo, 6 y 4, y el resultado lo dividiremos
entre el dato conocido de la segunda razón. Así, en nuestro ejemplo,
tendremos:
6 X 4 = 24
24 / 3 = 8
24 / 2 = 12
24 / 1 = 24
Así tendremos las proporciones siguientes:
6:4 = 8:3
6:4 = 12:2
6:4 = 24:1
Con
lo que podemos calcular que para producir los 8 sillones en tres días,
necesitamos 8 trabajadores; para fabricarlos en dos días, necesitamos 12
trabajadores, y para hacerlos en 1 día, necesitamos 24 trabajadores.
Ejemplos de razones
- En
una caja tenemos 45 canicas azules y 105 canicas rojas. La expresamos
como 45:105 y dividiendo entre 15, tenemos que la razón es de 3:7 (tres
por cada siete), o sea, tres canicas azules por cada siete canicas
rojas.
- En una clase de un colegio cada pelota es utilizada por
cada equipo de cinco niños, o sea que tenemos cinco alumnos por cada
pelota de fútbol. Tenemos entonces en este ejemplo de razón que la
relación entre alumnos – pelotas es 5 a 1. Esta razón se escribe 5:1 y
concluimos que existe una razón de cinco alumnos por cada pelota de
fútbol.
- En un estacionamiento hay coches de fábricas asiáticas y
de fábricas americanas. En total hay 3060 coches, de los cuales, 1740
son de fabricación asiática y el resto, 1320, son de fabricación
americana. Esto nos dará que la razón es de 1740/1320. Para
simplificarla, la dividimos primero entre 10, lo que nos deja 174/132.
Si ahora lo dividimos entre 6, tendremos la razón 29:22, o sea que en el
estacionamiento hay 29 automóviles asiáticos por cada 22 automóviles
americanos.
Ejemplos de proporciones:
Proporción directa:
- En
una tienda se venden dulces nacionales e importados, a razón de 3:2 Si
sabemos que al día se vende 255 dulces nacionales, ¿Cuántos dulces
importados se venden al día?
3:2=256:?
2 X 255 = 510
510 / 3 = 170 dulces importados.
3:2 = 256:170 (tres es a dos como 256 es a 170).
- En
una fiesta se invitaron a niños y niñas. Si sabemos que acudieron en
una proporción de 6 niñas por cada 4 niños, y en la fiesta hay 32 niños
¿Cuántas niñas fueron?
6:4 = ?:32
32 X 6 = 192
192 / 4 = 48 niñas fueron a la fiesta.
6:4 = 48:32 (6 es a 4 como 48 es a 32)
- Para armar una mesa, se necesitan 14 tornillos. ¿Cuántos tornillos necesitamos para armar 9 mesas?
14:1 = ?:9
14 X 9 = 126
126 / 1 = 126 tornillos son necesarios.
14:1 = 126:9 (14 es a 1 como 126 es a 9)
Proporción inversa:
- Dos grúas mueven 50 contenedores en hora y media. ¿Cuántas grúas se necesitan para mover los 50 contenedores en media hora?
2:1.5 =?:.5
2 X 1.5 = 3
3 / .5 = 6 grúas son necesarias.
2:1.5 = 6:.5 (dos grúas es a una hora y media, como seis grúas son a media hora)
Si
4 alumnos realizan un trabajo en equipo en 45 minutos ¿Cuánto tiempo
tardarán si el equipo está formado por 6, 8, 10 y 12 estudiante
acuntinuacion un video para mayor entendimiento
unidad #3
numeros reales
valor absoluto
Definición de valor absoluto
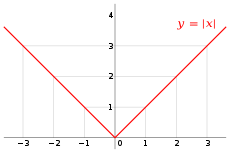
Gráfica de la función valor absoluto.
El valor absoluto es una función que representa la distancia de un punto al origen. Si tomamos un punto cualquiera x y este es positivo, la distancia de x al origen 0 es igual a x; si fuera negativo, la distancia de x al origen 0 es igual a -x.
Esto se debe a que una distancia no puede ser negativa, ya que no
tendría sentido. Todas las distancias son positivas y por lo mismo, el
valor absoluto de un número, que es una distancia, debe ser positivo.
De manera mas forma
EJEMPLOS DE VALOR ABSOLUTO:
a) (3) = 3, porque 3 > O
b) (-3 )= - (-3) = 3, porque -3 < O tomamos su inverso
c) Si ( x ) = 3 entonces x = 3 óx= -3
e) (x-1)=5 por lo tanto x-1=5 ó x-1= -5
x-1 =5 por lo tanto x=6
x-1=-5 por lo tanto x=-4
ecuaciones
Una ecuación es una igualdad matematica entre dos expresciones denominadas miembros y separadas por el signo igual , en las que aparecen elementos conocidos o datos
desconocidos o incognitas relacionados mediante operaciones
matematicas Los valores conocidos pueden ser numeros , coeficientes o
constantes también variables
o incluso objetos complejos como funciones o vectores, los elementos
desconocidos pueden ser establecidos mediante otras ecuaciones de un
sistema , o algún otro procedimiento de resolución de ecuaciones.Las
incógnitas, representadas generalmente por letras, constituyen los
valores que se pretende hallar (en ecuaciones complejas en lugar de
valores numéricos podría tratarse de elementos de un cierto conjunto
abstracto, como sucede en lasecuaciones diferenciales Por ejemplo, en
la ecuaciones algebraicas simple:

la variable  representa la incógnita, mientras que el coeficiente 3 y los números 1 y
9 son constantes conocidas. La igualdad planteada por una ecuación será
cierta o falsa dependiendo de los valores numéricos que tomen las
incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables (incógnitas) la hacen cierta.
Se llama solución de una ecuación a cualquier valor individual de dichas variables que la satisfaga. Para el caso dado, la solución es:
representa la incógnita, mientras que el coeficiente 3 y los números 1 y
9 son constantes conocidas. La igualdad planteada por una ecuación será
cierta o falsa dependiendo de los valores numéricos que tomen las
incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables (incógnitas) la hacen cierta.
Se llama solución de una ecuación a cualquier valor individual de dichas variables que la satisfaga. Para el caso dado, la solución es:

En
el caso de que todo valor posible de la incógnita haga cumplir la
igualdad, la expresión se llama identidad . Si en lugar de una igualdad
se trata de una desigualdad entre dos expresiones matemáticas, se
denominará inecuacion .
ejemplos
ecuaciones lineales o de primer grado
Las ecuaciones lineales o de primer grado son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.
Resolución de ecuaciones lineales
En general para resolver una ecuación lineal o de primer grado debemos seguir los siguientes pasos:
1º Quitar paréntesis.
2º Quitar denominadores.
3º Agrupar los términos en x en un miembro y los términos independientes en el otro.
4º Reducir los términos semejantes.
5º Despejar la incógnita.
Ejemplos de ecuaciones lineales
Despejamos la incógnita:
Agrupamos los términos semejantes y los independientes, y sumamos:
Quitamos paréntesis:
Agrupamos términos y sumamos:
Despejamos la incógnita:
Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.
Quitamos paréntesis, agrupamos y sumamos los términos semejantes:
Despejamos la incógnita:
Quitamos paréntesis y simplificamos:
Quitamos denominadores, agrupamos y sumamos los términos semejantes:
Quitamos corchete:
Quitamos paréntesis:


































![{\displaystyle {\sqrt[{3}]{\frac {8}{27}}}={\frac {\sqrt[{3}]{8}}{\sqrt[{3}]{27}}}={\frac {2}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bc1e4b0013f1cbef0e01ec7728a89c3dd0141b5)