unidad # 3

numeros reales

3.1 conjuntos numericos

Resultado de imagen de conjuntos de numeros complejos

Comenzaremos por estudiar tres conjuntos en particular, los números naturales, los números enteros y los números racionales o fraccionarios.
Estos conjuntos de números han ido apareciendo a medida que la humanidad se ha visto en la necesidad de solucionar problemas y retos cada vez más complejos y más profundos.

No existe una notación universal para indicarlos, como

\mathbb{I}

, que es generalmente aceptada. Las razones son que el conjunto de Números Irracionales no constituyen alguna estructura algebraica , como sí lo son los naturales (

\mathbb{N}

), los enteros (

\mathbb{Z}

), los racionales (

\mathbb{Q}

), los reales (

\R

) y los complejos (

\mathbb{C}

), por un lado, y que la

\mathbb{I}

es tan apropiada para designar al conjunto de Números Irracionales como al conjunto de numeros imaguinarios puros lo cual puede crear confusión. Fuera de ello,

$\mathbb {I} :=\mathbb {R} \backslash \mathbb {Q} =\{x\in \mathbb {R} |x\notin \mathbb {Q} \}$

operaciones entre numeros reales

Un conjunto es una colección de objetos considerada como un objeto en sí. Un conjunto está definido únicamente por los elementos que lo componen, y no por la manera en la que se lo representa.
Existe una serie de relaciones básicas entre conjuntos y sus elementos:

Pertenencia. La relacion relativa a conjuntos más básica es larelacion de pertenencia Dado un elemento $x$ , éste puede o no pertenecer a un conjunto dado $A$ . Esto se indica como $x \in A$ .
Igualdad. Dos conjuntos son iguales si y sólo si tienen los mismos elementos. Este principio, denominado principio de exterioridad establece el hecho de que un conjunto queda definido únicamente por sus elementos.
inclusion. Dado un conjunto $A$ , cualquier subcolección $B$ de sus elementos es un subconjunto de $A$ , y se indica como $B \subseteq A$ .

El conjunto vacio es el conjunto sin ningún elemento, y se denota por

\emptyset

o por {}. El cunjunto universal es el conjunto que contiene todos los elementos posibles, dentro del contexto considerado. Por ejemplo, si se estudian los números naturales, el conjunto universal es el conjunto de todos ellos,

N

. De manera general, el conjunto universal se denota por

U

Ejemplos

Cada numero natural l es elemento del conjunto $N = {1, 2, 3, ...}$ de los números naturales: $1 \in N$ , $2 \in N$ , etc. Cada numero par es también un número natural, por lo que el conjunto $P$ de los números pares, $P = {2, 4, 6, ...}$ , es un subconjunto de $N$ : $P \subseteq N$ .
Dado el conjunto de letras $V = {o, i, e, u, a}$ , se cumple por ejemplo que $a \in V$ o también $i \in V$ . El conjunto de letras $U = { vocales del español }$ contiene los mismos elementos que $V$ , por lo que ambos conjuntos son iguales, $V = U$ .

¿Qué son los números naturales?

Cuando el hombre tuvo la necesidad de ordenar conjuntos y saber la cantidad de elementos que los conformaban, así aparecieron los números naturales.

Para negociar y ordenar cosas, el hombre tuvo la necesidad de representar las cantidades de lo que tenía para saber con qué contaba exactamente. De ahí surgió la necesidad de crear símbolos que representaran esas cantidades.

Ejemplos

Cada numero natural l es elemento del conjunto $N = {1, 2, 3, ...}$ de los números naturales: $1 \in N$ , $2 \in N$ , etc. Cada numero par es también un número natural, por lo que el conjunto $P$ de los números pares, $P = {2, 4, 6, ...}$ , es un subconjunto de $N$ : $P \subseteq N$ .
Dado el conjunto de letras $V = {o, i, e, u, a}$ , se cumple por ejemplo que $a \in V$ o también $i \in V$ . El conjunto de letras $U = { vocales del español }$ contiene los mismos elementos que $V$ , por lo que ambos conjuntos son iguales, $V = U$ .

¿que son numeros irracionales?

En matematicas , un número irracional es un número que no puede ser expresado como una fracción ^m⁄_n, donde

m

n

sean enteros y

n

sea diferente de cero.¹ Es cualquier numero real que no es racional, y su expresión decimal no es ni exacta ni periódica.¹
Un decimal infinito (es decir, con infinitas cifras) aperiódico, como √7 = 2,645751311064591 no puede representar un número racional. A tales números se les nombra "números reales o irracionales". Esta denominación significa la imposibilidad de representar dicho número como razón de dos números enteros.² El numero irracional (

\pi

). (

\phi

) son otros ejemplos de números irracionales.

Ejemplos de números irracionales

π (pi): Este es quizás el número irracional más conocido de todos. Se trata de la expresión de la relación que existe entre el diámetro de una esfera y su longitud. Pi entonces es 3.141592653589 (…), aunque en general se lo conoce simplemente como 3.14.
√5: 2.2360679775
√123: 11.0905365064
e: se trata del número de Euler y se trata de la curva que se observa en los tejidos eléctricos y que figura en procesos tales como las radiaciones radiactivas o bien en los procesos de crecimiento. El número de Euler es: 2.718281828459 (…).
√3: 1.73205080757
√698: 26.4196896272

Números Racionales

Los numeros racionales son todos los números que son susceptibles de ser expresados como una fraccion , es decir, como el cociente de dos números enteros. La palabra ‘racional’ deriva de la palabra ‘razón’, que significa proporción o cociente.
En las operaciones matemáticas que se hacen a diario para resolver cuestiones cotidianas, casi todos los números que se manejan son racionales, pues la categoría abarca a todos losnumeros enteros y a una gran parte de los que llevan decimales .
Tanto los números fraccionarios racionales como los irracionales (su contraparte) son categorías infinitas. Sin embargo, estos se comportan de diferente manera: los números racionales son comprensibles y, en tanto representables por fracciones, su valor se puede aproximar con un criterio simplemente matemático, no ocurre esto con los irracionales.

Ejemplos de números racionales

Aquí se listan números racionales a modo de ejemplo. En los casos de ser estos a su vez números fraccionarios, se indica también su expresión como cociente:

142
3133
10
31
69,96 (1749/25)
625
7,2 (36/5)

numeros complejos

ejemplos

Números complejos

Un número complejo es una combinación de un número real y un número imaginario

Ejemplos:

1 + i

12 - 3.1i

-0.85 - 2i

π + πi

√2 + i/2

¿ que son numeros imaguinarios?

En matemáticas, un número imaginario es un numero complejo cuya parte real es igual a cero, por ejemplo:

5i\

es un número imaginario, así como

i\

-i\

son también números imaginarios. En otras palabras, es un número de la forma:

z = x + y \, i \; : \quad x = 0

los números imaginarios pueden describirse como el producto de un número real por la unidad imaginaria i, en donde la letra i denota la raiz cuadrada de _1

$i = \sqrt{-1}$

Operaciones con conjuntos

conjuntos

Unión

Intersección

Diferencia

Complemento

Diferencia simétrica

Las operaciones básicas del álgebra de conjuntos son:

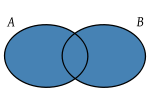
Unión. de dos conjuntos $A$ y $B$ es el conjunto $A \cup B$ que contiene todos los elementos de $A$ y de $B$
Intersección de dos conjuntos $A$ y $B$ es el conjunto $A \cap B$ que contiene todos los elementos comunes de $A$ y $B$ .
Diferencia. entre dos conjuntos $A$ y $B$ es el conjunto $A \ B$ que contiene todos los elementos de $A$ que no pertenecen a $B$ .
Diferencia simétrica. La diferencia simétrica entre dos conjuntos $A$ y $B$ es el conjunto que contiene los elementos de $A$ y $B$ que no son comunes.
Complemento. de un conjunto $A$ es el conjunto $A ∁$ que contiene todos los elementos que no pertenecen a $A$ .
Producto cartesiano. de dos conjuntos $A$ y $B$ es el conjunto $A \times B$ que contiene todos los pares ordenados (a, b) cuyo primer elemento pertenece a $A$ y su segundo elemento pertenece a $B$ .

Propiedades

Algunas de estas operaciones poseen propiedades similares a las operaciones con números naturales.
Por ejemplo, la unión y la intersección son conmutativas asociativas . El conjunto vacío es elemento neutro de la unión, y el elemento del absorbente de la intersección y el producto cartesiano.
El conjunto universal es el elemento neutro de la intersección y el elemento absorbente de la unión.
Además, las operaciones de unión, intersección, diferencia y complemento son muy similares a las operaciones en un algebra así como a los conectores loguicos .

expresiones algebraicas

Recibe el nombre de expresiones algebraica, a aquella enunciación, expuesta en lenguaje matemático, formada por números y por simbolos representados por letras (indicadores de incógnitas, pues indican cantidades que se deben averiguar) que se encuentran vinculados entre sí por medio de signos, que señalan las operaciones que se necesitan efectuar, ya sean sumas, restas, multiplicaciones, divisiones o potenciaciones.
En álgebra se resuelven operaciones para grandes conjuntos numéricos, y no en cada caso concreto, como sucede en la aritmética. Para hacerlo, se ayuda con letras.

Al sustituirse las incógnitas o variables por los números correspondientes, realizándose la operación requerida, se obtiene el valor numérico que permite obtener un resultado numérico, que se usa por ejemplo para encontrar áreas o volúmenes. El número que aparece a la izquierda de la incognita variable, se llama coeficiente, que se omite si se trata de la unidad.

Cuando la expresión algebraica cuenta con un solo término se denomina monomio, si son dos, binomio, en el caso de tres, trinomio. Cuando posee más de tres términos, se denomina polinomio, que en realidad es la denominación que puede aplicarse siempre que exista más de un término.
Si la expresión algebraica no tiene denominador y las letras tienen solamente potencias naturales, se dice que es entera; y fraccionaria en caso contrario. Si bajo el signo radical, no tiene letras, se llama racional, y si las tiene, se denomina irracional.

Dos expresiones algebraicas separadas por el signo de igualdad (=) se llama ecuación, por ejemplo 4x+5 = 17. El valor que en este caso satisface la incógnita, es 3, ese valor se conoce como solución o raíz. La parte de la ecuación colocada antes, o sea, a la izquierda del signo de igualdad, se denomina premier miembro, y lo que se escribe a la derecha, segundo miembro.

terminos de expresiones alguebraicas

ejemplos de expresiones alguebraicas

Términos:

3a²b⁵ + 7y² - abc⁶
6x² + 98y³

2.- Monomios:

9a³b⁴
19n²9¹
17xy+5k²

3.- Trinomios:

3n5y³ +23n⁵y8z³– π²
3n - 22ª²+ 26n⁴
xy + 18n³- 2x²

4.- Polinomios (más de tres términos):

3n5y³ +23n⁵y8z³– π² 3n - 22ª²+ 26n⁴
xy + 18n³- 2x²- 9a³b⁴- 19n²9¹+17xy+5k²
3a²b⁵ + 7y² - abc⁶+ 6x² + 98y³

ejemplos de axpresiones alguebraicas grado de minomios y polinomios

El exponente en 3x² es 2

El exponente en 5x⁴ es 4

El exponente en -2 es 0, porque -2=-2x⁰ (x⁰=1)

Entonces el grado de es 4, el exponente de mayor orden de la variable en el polinomio.

De manera semejante, el grado de es 5, puesto que 5 es el exponente de mayor orden de una variable presente en el polinomio.

Por convención, un número como -4 o 7 se conoce como polinomio de grado 0, porque si a¹0, a=ax°.

El grado de un polinomio puede ser “absoluto” o “relativo” a una literal.

Grado absoluto: El grado absoluto de un polinomio se determina por el exponente mayor, de uno de sus términos.

El grado absoluto es cuatro.

El grado absoluto es sexto.

El grado absoluto es quinto.

Grado relativo a una literal: El grado relativo de un polinomio con respecto a una literal, es el mayor exponente que tiene la literal que se considere del polinomio.

El grado con relación a x es séptimo, de quinto grado con relación a y.

El grado con relación a a es tres, de segundo grado con relación a b.

Polinomio cero

El mismo número 0 se conoce como polinomio cero y no se le asigna grado. Se hace notar que 0×x⁴=0, 0×x²=0, 0×x³=0, y así sucesivamente de modo que los polinomios cero no pueden tener grado.

ejemplos de multiplicacion , division y restas de monomios

Sustracción de monomios

Para restar monomios, se suma el minuendo con el sustraendo cambiado de signo y se da el mismo proceso de la suma.

ejemplo: Sean los monomios

x^{3}

3x^{3}

su resta sería:

x^{3}-(+3x^{3})=x^{3}+(-3x^{3})=-2x^{3}

Multiplicación de monomios

Para multiplicar monomios, se suman los exponentes de cada variable, se multiplican los números, y se juntan todas las variables.

Ejemplo:

5x^{3}.3y^{2}x=15x^{4}y^{2}

4z^{2}.2z^{3}y=8z^{5}y

1w^{4}.1y^{4}=1w^{4}y^{4}

División de monomios

Para dividir monomios, se resta los exponentes de cada variable, se dividen los números, y se agrupan todas las variables o incógnitas.
Ejemplo:

8x^{4}y/2x^{2}=4x^{2}y

4z^{2}/2z^{3}=2/z

^–1

1w^{4}/1y^{4}=1w^{4}/y^{4}

Potencia de monomios

Para realizar la potencia de monomios, se multiplica el coeficiente tantas veces como indica la potencia y se multiplica los exponentes por la potencia.
Ejemplo: (

5x^{3})^{2}=25x

^3×2

^{$=25x^{6}$}

Multiplicación de fracciones

Para multiplicar dos fracciones, unicamente es multiplicar el numerador de la primera fracción con el numerador de la segunda fracción, y hacer lo mismo con los denominadores.

{\frac {3}{6}}\cdot {\frac {2}{5}}={\frac {3\cdot 2}{6\cdot 5}}={\frac {6}{30}}

Multiplicación de una fraccion con un número natural

Para multiplicar una fracción con un número se multiplica el número con el numerador, y el denominador por 1, ya que el número es una fracción con denominador 1:

6\cdot {\frac {1}{3}}={\frac {6}{1}}\cdot {\frac {1}{3}}={\frac {6\cdot 1}{1\cdot 3}}={\frac {6}{3}}=2

Multiplicación de dos fracciones

Para multiplicar dos fracciones, se multiplican los denominadores y los numeradores por los denominadores y los numeradores de las fracciones restantes

{\frac {1}{3}}\cdot {\frac {2}{5}}\cdot {\frac {4}{7}}\cdot {\frac {6}{8}}={\frac {1\cdot 2\cdot 4\cdot 6}{3\cdot 5\cdot 7\cdot 8}}={\frac {48}{840}}

Multiplicación de fracciones inversas

Cuando dos fracciones inversas se multiplican, el resultado es la unidad.

{\frac {3}{6}}\cdot {\frac {6}{3}}={\frac {3\cdot 6}{6\cdot 3}}={\frac {18}{18}}=1

Otras operaciones con fracciones

Potenciacion de fracciones

Hay que decir que una potencia es aquella multiplicación donde se multiplica la base por si misma tantas veces como lo indique el exponente. Por lo que es una multiplicación de fracciones.

\left({\frac {1}{2}}\right)^{3}={\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}={\frac {1^{3}}{2^{3}}}={\frac {1}{8}}

Radicación de fracciones

La radicación es el proceso inverso a la potenciación. Para radicar una fracción, se extrae la raiz enesíma al numerador y denominador.

{\sqrt[{3}]{\frac {8}{27}}}={\frac {\sqrt[{3}]{8}}{\sqrt[{3}]{27}}}={\frac {2}{3}}

{\sqrt {\frac {16}{20}}}={\frac {\sqrt {16}}{\sqrt {20}}}={\frac {4}{\sqrt {20}}}

Racionalización

En el caso anterior, comprobamos que el denominador tenía una raiz cuadrada en su denominador. Para evitar tal situacion, se debe multiplicar la fracción con su conjugada para hacer desaparecer la raiz en el denominador.

{\frac {4\cdot {\sqrt {20}}}{{\sqrt {20}}\cdot {\sqrt {20}}}}={\frac {4{\sqrt {20}}}{20}}={\frac {\sqrt {20}}{5}}

Existe el caso en el que el denominador tiene una suma de un número entero con un radical. Para racionalizar, la conjugada debe completar una diferencia de cuadrados.

{\frac {3-{\sqrt {2}}}{3+{\sqrt {2}}}}={\frac {(3-{\sqrt {2}})(3-{\sqrt {2}})}{(3+{\sqrt {2}})(3-{\sqrt {2}})}}={\frac {(3-{\sqrt {2}})^{2}}{(3+{\sqrt {2}})(3-{\sqrt {2}})}}={\frac {9+2-6{\sqrt {2}}}{9-2}}={\frac {11-6{\sqrt {2}}}{7}}

acontinuacion video para mayor entendimiento

Cálculo del máimo común divisor y mínimo común múltiple

MÁXIMO COMÚN IVISOR:
El Máximo Común Divisor es, como su nombre indica, el mayor de los divisores comunes de varios números. Para calcularlo, se descompone cada uno de ellos en factores primos. El M.C.D. es el resultado de multiplicar los factores que se repitan en todas las descomposiciones, afectados por el menor exponente.
En el caso de que no se repita ningún factor, el M.C.D. de esos números es 1, y se dice que los números son “primos entre sí”. Por ejemplo, el 18 y el 25 son primos entre sí.

Ejemplos:

Si queremos hallar el M.C.D. de 36, 60 y 72, descomponemos los tres en factores primos:

36 = 2²·3²
60 = 2²·3·5
72 = 2³·3²
Vemos que los únicos factores que se repiten en las tres descomposiciones son el 2 y el 3. Los cogemos con los menores exponentes al que están afectados, por lo que el M.C.D. será 2²·3 = 12.

M.C.D.(36, 60, 72) = 12

Para hallar el M.C.D. de 18 y 25:

18 = 2·3²
25 = 5²
No hay ningún factor repetido, luego:

M.C.D.(18, 25) = 1

Los números 18 y 25 son primos entre sí.
MÍNIMO COMÚN MÚLTIPLO:

El Mínimo Común Múltiplo es, así mismo, el menor de los múltiplos comunes a varios números. Para calcularlo, descomponemos los números en factores primos, y el M.C.M es el resultado de multiplicar los factores comunes y los no comunes, afectados por el mayor exponente.
Si los números son primos entre sí, el M.C.M. es el producto entre ellos.

Ejemplos:

El M.C.M de 36, 60 y 72, que ya tenemos descompuestos más arriba. Los factores que se repiten son el 2 y el 3, y los que no se repiten, el 5. Los cogemos con los mayores exponentes, es decir, 2³, 3² y 5. El M.C.M. es, por lo tanto:

M.C.M.(36, 60, 72) = 2³·3²·5 = 360

El M.C.M. de 18 y 25. Como no se repetía ningún factor, tenemos que cogerlos todos, afectados con el exponente que llevan, es decir, estamos cogiendo todos los factores, por lo que el M.C.M. es el producto de 18·25:

M.C.M.(18, 25) = 2·3²·5² = 450

aqui veremos acontinuacion un video sobre lo planteado

opereraciones aritmeticas

Suma o adición

La suma es una operación que se deriva de la operación de contar.
Si tenemos 6 ovejas y compramos 2 ovejas ¿cuantas ovejas tenemos?. Una forma de hacerlo sería volver a contar todas las ovejas, pero alguien que hubiese contado varias veces el mismo caso, recordaria el resultado y no necesitaría volver a contar las ovejas. Sabria que 6 + 2 = 8.
Los términos de la suma se llaman sumandos.

Propiedades de la suma:

a + b = b + a Esta propiedad se llama conmutativa.
Si tenemos que sumar varios numeros podemos hacerlo en cualquier orden (esto se llama propiedad asociativa). Si tenemos que sumar a, b, c y d, podemos sumar primero a + b, despues c + d y despues sumar los dos resultados anteriores, o podemos sumar a + c, despues b + d y despues sumar los dos resultados anteriores o podemos sumar a + b y al resultado sumarle c y al resultado sumarle d. En fin podemos sumar los numeros en cualquier orden.
La suma tiene elemento neutro. El cero es el elemento neutro de la suma porque siempre se cumple que a + 0 = a.
La suma tiene elemento simétrico. El elemento simetrico de un número es otro que sumado al anterior da el elemento neutro. El elemento simetrico de a es -a, porque a + (-a) = 0

Resta o substración

Igual que la suma la resta es una operacion que se deriva de la operacion de contar.
Si tenemos 6 ovejas y los lobos se comen 2 ovejas ¿cuantas ovejas tenemos?. Una forma de hacerlo sería volver a contar todas las ovejas, pero alguien que hubiese contado varias veces el mismo caso, recordaria el resultado y no necesitaría volver a contar las ovejas. Sabria que 6 - 2 = 4.
Los terminos de la resta se llaman minuendo (las ovejas que tenemos) y sustraendo (las ovejas que se comieron los lobos).

Propiedades de la resta:

La resta no tiene la propiedad conmutativa (no es lo mismo a - b que b - a)

Producto o multiplicación

Muchas veces tenemos que sumar un número consigo mismo varias veces. Por ejemplo, si tenemos que sumar 5 + 5 + 5 + 5 + 5 + 5 + 5, sería más breve representarlo asi 5 * 7 (esto significaria sumar 5 condigo mismo 7 veces).
La multiplicación es una forma abreviada de hacer un tipo especial de sumas.
Los terminos de la multiplicación se llaman multiplicando (el numero que se suma) y multiplicador (el número de veces que se suma).
Propiedades de la multiplicación
a * b = b * a. Esta propiedad se llama propiedad conmutativa
Si tenemos que multiplicar varios numeros podemos hacerlo en cualquier orden (esto se llama propiedad asociativa). Si tenemos que multiplicar a, b, c y d, podemos multiplicar primero a . b, despues c . d y despues multiplicar los dos resultados anteriores, o podemos multiplicar a . c, despues b . d y despues multiplicar los dos resultados anteriores o podemos multiplicar a . b y multiplicar el resultado por c y despues multiplicarlo por d. En fin podemos multiplicar los numeros en cualquier orden.
La multiplicación tiene elemento neutro. El uno es el elemento neutro de la multiplicación porque siempre se cumple que a .1 = a.
La multiplicación tiene elemento simétrico. El elemento simetrico de un número es otro que multiplicado por el anterior da el elemento neutro. El elemento simetrico de a es 1/a, porque a / a = 0
a(b + c) = a . c + a . d. Esta propiedad se llama distributiva respecto a la suma.

División

La división es la operación que tenemos que hacer para repartir un numero de cosas entre un número de personas.
Los terminos de la división se llaman dividendo (el número de cosas), divisor (el número de personas), cociente (el numero que le corresponde a cada persona) y resto (lo que sobra).
Si el resto es cero la división se llama exacta y en caso contrario inexacta.

Propiedades de la division

La divisón no tiene la propiedad conmutativa. No es lo mismo a/b que b/a.

Potenciación

En bastantes ocasiones tenemos que multiplicar un número por si mismo un número dado de veces.
Por ejemplo: 5 * 5 * 5 * 5 * 5 * 5 * 5
Una forma de representar esta operacion es 5⁷ (esto quiere decir que hay que multiplicar 5 por si mismo 7 veces).
El numero inferior se llama base y el superior exponente.

Propiedades de la potenciación:

a^m.aⁿ= a^m+n
a^m/aⁿ= a^m-n
a⁰ = 1 (se deriva de la propiedad anterior a^m/a^m= 1 = a^m-m = a⁰)
(a^m)ⁿ = a^m.n
(a.b.c)^m = a^m . b^m .c^m
a^-n = 1/aⁿ (se deriva de la segunda propiedad).

Radicación

La radicacion es la operacion inversa de la potenciación. Supongamos que nos dan un número a y nos piden calcular otro, tal que, multiplicado por si mismo un número b de veces nos da el numero a.
Por ejemplo: calcular qué número multiplicado por si mismo 2 veces da 196. Ese número es 14.
El número que esta dentro de la raiz se llama radicando, el grado de la raiz se llama índice del radical, el resultado se llama raiz.
Podemos considerar la radicación como un caso particular de la potenciación. En efecto, la raiz cuadrada de un numero (por ejemplo a) es igual que a^1/2, del mismo modo la raiz cúbica de a es a^1/3 y en general, la raiz enesima de un numero a es a^1/n.
La mejor forma de resolver los ejercicios de operaciones con raices es convertir las raices a potencias y operar teneiendo en cuenta las propiedades dadas para la operacion de potenciación.

representacion fraccionaria

Representación de números racionales en la recta numérica
Para representar los números racionales en la recta numérica, tienes que comparar los números dados, para lo cual deberás transformar de número decimal a fracción o de fracción a número decimal.

1.1- Representación de números decimales en la recta numérica
Si tienes que transformar las fracciones a número decimal, puedes ubicar los números racionales en la recta numérica de la siguiente forma; si son números negativos y positivos dibuja una recta dividida en 2 mitades simétricas desde el origen, es decir, desde el número 0. A la izquierda del número 0 ubicas los números negativos y a la derecha los números positivos, de menor a mayor, manteniendo la misma distancia entre dos números consecutivos. Para ubicar los décimos se divide la distancia entre dos números consecutivos en 10 partes iguales. Los números decimales inexactos los puedes aproximar para que sea más fácil ubicarlos.

recta_numeros_racionales_0.jpg (485×107)

Una vez que ubiques todos los decimales en la recta numérica, puedes anotar los números racionales originales.
Recuerda que, los números positivos mientras más cerca del cero menor será su valor y los números negativos mientras más cerca del cero mayor será su valor.
Ejemplo: Representa los siguientes números racionales en la recta numérica;

- Primero debes transformar las fracciones a números decimales y el número mixto a fracción impropia y luego a número decimal.

recta_numeros_racionales_2.jpg (506×385)

Recuerda: Para transformar un número mixto a fracción impropia debes multiplicar el entero por el denominador y sumar el numerador, este resultado se escribe en el numerador y el denominador se mantiene igual.

Ejemplo:

- Entonces los números que tienes que representar son los siguientes;

recta_numeros_racionales_4.jpg (505×31)

- Aproxima los números decimales inexactos, los que tienen centésimos también los puedes aproximar. En este caso no aproximaremos, ya que, sabemos que (0,05) se ubica en la mitad entre dos décimos de la recta que dibujaremos.

recta_numeros_racionales_5.jpg (558×143)

- Ahora puedes comparar y ubicar los números decimales en la recta numérica.

- Anota los números racionales originales en la recta numérica.

recta_numeros_racionales_7.jpg (495×116)

razones y proporciones

Las razones y proporciones, nosotros denominamos razón al cociente que es indicado por dos números y que representa la relación entre dos cantidades y una proporción a la igualdad que existe entre dos o más razones.

Razón. Una razón indica en forma de división la relación entre dos cantidades. Nos indica cuántas unidades hay en relación a las otras, y se suele indicar simplificando las fracciones.
Por ejemplo, si en un salón de clases tenemos 24 niñas y 18 niños, entonces lo representaremos de alguna de las siguientes formas:

24/18
24:18

Y como la fracción podemos simplificarla al dividirla entre 6, entonces tendremos:

4/3
4:3

Y se lee que existe una razón de 4 a 3, o de 4 por cada 3.
Cada uno de los valores de una razón tiene un nombre. El valor que está del lado izquierdo de la relación, se le llama antecedente, y al valor del lado derecho se le llama consecuente.
En este caso, la relación de niñas respecto a los niños es una relación de 4 a 3, o de 4 niñas por cada 3 niños.

Proporción. La proporción indica mediante una igualdad la comparación de dos razones. Para escribir una proporción, debemos tener en cuenta que los valores antecedentes, siempre estén del mismo lado, al igual que los consecuentes.
En nuestro ejemplo del salón de clases, podemos comparar la razón que tenemos, de 4 niñas por cada 3 niños, y podremos calcular cuántos niños hay en un salón en relación al número de niñas o viceversa. Para esto, en primer lugar escribiremos la proporción que ya conocemos:

4:3

Después, un signo de igualdad

4:3=

Y después la cantidad total, por ejemplo la del mismo salón, recordando que debemos respetar el orden del antecedente y del consecuente. En nuestro ejemplo, el antecedente será el número de niñas, y el consecuente el número de niños.

4:3=24:18

Para comprobar la igualdad de la proporción, se efectúan dos multiplicaciones. En una proporción, tomaremos como referencia el signo de igualdad. Los números que están más cercanos, se llaman centros, y los números más lejanos son los extremos. En nuestro ejemplo, los números 3 y 24 son los más cercanos al signo igual, por lo que son los centros. El 4 y el 18, son los extremos. Para comprobar que la proporción es correcta, el producto de la multiplicación de los centros debe ser igual al producto de la multiplicación de los extremos:

3 X 24 = 72
4 X 18 = 72

Proporción directa y proporción inversa:
Las proporciones pueden expresar relaciones en que el aumento de la cantidad del antecedente aumenta la cantidad del consecuente. A esta variación se le llama proporción directa. El ejemplo anterior es una proporción directa.
En una proporción inversa, el aumento de la cantidad en el antecedente, significa la disminución de la cantidad en el consecuente.
Por ejemplo, en una mueblería, 6 trabajadores hacen 8 sillones en 4 días. Si queremos saber cuántos trabajadores se necesitan para construir los 8 sillones en 1, 2 y 3 días, usaremos una proporción inversa.
Para determinarla, usaremos el número de trabajadores como cifra antecedente, y el número de días como cifra consecuente
:

6:4=

Siguiendo el mismo orden, del otro lado de la igualdad tendremos como antecedente nuevamente el número de trabajadores, y como consecuente los días que tardarán. Tendremos algo como lo siguiente:

6:4 = ?:3
6:4 = ?:2
6:4 = ?:1

Para determinar la proporción inversa, multiplicaremos los factores de la razón conocida, en nuestro ejemplo, 6 y 4, y el resultado lo dividiremos entre el dato conocido de la segunda razón. Así, en nuestro ejemplo, tendremos:

6 X 4 = 24
24 / 3 = 8
24 / 2 = 12
24 / 1 = 24

Así tendremos las proporciones siguientes:

6:4 = 8:3
6:4 = 12:2
6:4 = 24:1

Con lo que podemos calcular que para producir los 8 sillones en tres días, necesitamos 8 trabajadores; para fabricarlos en dos días, necesitamos 12 trabajadores, y para hacerlos en 1 día, necesitamos 24 trabajadores.

Ejemplos de razones

En una caja tenemos 45 canicas azules y 105 canicas rojas. La expresamos como 45:105 y dividiendo entre 15, tenemos que la razón es de 3:7 (tres por cada siete), o sea, tres canicas azules por cada siete canicas rojas.
En una clase de un colegio cada pelota es utilizada por cada equipo de cinco niños, o sea que tenemos cinco alumnos por cada pelota de fútbol. Tenemos entonces en este ejemplo de razón que la relación entre alumnos – pelotas es 5 a 1. Esta razón se escribe 5:1 y concluimos que existe una razón de cinco alumnos por cada pelota de fútbol.
En un estacionamiento hay coches de fábricas asiáticas y de fábricas americanas. En total hay 3060 coches, de los cuales, 1740 son de fabricación asiática y el resto, 1320, son de fabricación americana. Esto nos dará que la razón es de 1740/1320. Para simplificarla, la dividimos primero entre 10, lo que nos deja 174/132. Si ahora lo dividimos entre 6, tendremos la razón 29:22, o sea que en el estacionamiento hay 29 automóviles asiáticos por cada 22 automóviles americanos.

Ejemplos de proporciones:

Proporción directa:

En una tienda se venden dulces nacionales e importados, a razón de 3:2 Si sabemos que al día se vende 255 dulces nacionales, ¿Cuántos dulces importados se venden al día?

3:2=256:?
2 X 255 = 510
510 / 3 = 170 dulces importados.
3:2 = 256:170 (tres es a dos como 256 es a 170).

En una fiesta se invitaron a niños y niñas. Si sabemos que acudieron en una proporción de 6 niñas por cada 4 niños, y en la fiesta hay 32 niños ¿Cuántas niñas fueron?

6:4 = ?:32
32 X 6 = 192
192 / 4 = 48 niñas fueron a la fiesta.
6:4 = 48:32 (6 es a 4 como 48 es a 32)

Para armar una mesa, se necesitan 14 tornillos. ¿Cuántos tornillos necesitamos para armar 9 mesas?

14:1 = ?:9
14 X 9 = 126
126 / 1 = 126 tornillos son necesarios.
14:1 = 126:9 (14 es a 1 como 126 es a 9)

Proporción inversa:

Dos grúas mueven 50 contenedores en hora y media. ¿Cuántas grúas se necesitan para mover los 50 contenedores en media hora?

2:1.5 =?:.5
2 X 1.5 = 3
3 / .5 = 6 grúas son necesarias.
2:1.5 = 6:.5 (dos grúas es a una hora y media, como seis grúas son a media hora)

Si 4 alumnos realizan un trabajo en equipo en 45 minutos ¿Cuánto tiempo tardarán si el equipo está formado por 6, 8, 10 y 12 estudiante

acuntinuacion un video para mayor entendimiento

unidad #3

numeros reales

valor absoluto

Definición de valor absoluto

Gráfica de la función valor absoluto.

El valor absoluto es una función que representa la distancia de un punto al origen. Si tomamos un punto cualquiera x y este es positivo, la distancia de x al origen 0 es igual a x; si fuera negativo, la distancia de x al origen 0 es igual a -x.
Esto se debe a que una distancia no puede ser negativa, ya que no tendría sentido. Todas las distancias son positivas y por lo mismo, el valor absoluto de un número, que es una distancia, debe ser positivo.
De manera mas forma

EJEMPLOS DE VALOR ABSOLUTO:

a) (3) = 3, porque 3 > O
b) (-3 )= - (-3) = 3, porque -3 < O tomamos su inverso
c) Si ( x ) = 3 entonces x = 3 óx= -3
e) (x-1)=5 por lo tanto x-1=5 ó x-1= -5
x-1 =5 por lo tanto x=6
x-1=-5 por lo tanto x=-4

ecuaciones

Una ecuación es una igualdad matematica entre dos expresciones denominadas miembros y separadas por el signo igual , en las que aparecen elementos conocidos o datos desconocidos o incognitas relacionados mediante operaciones matematicas Los valores conocidos pueden ser numeros , coeficientes o constantes también variables o incluso objetos complejos como funciones o vectores, los elementos desconocidos pueden ser establecidos mediante otras ecuaciones de un sistema , o algún otro procedimiento de resolución de ecuaciones.Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar (en ecuaciones complejas en lugar de valores numéricos podría tratarse de elementos de un cierto conjunto abstracto, como sucede en lasecuaciones diferenciales Por ejemplo, en la ecuaciones algebraicas simple:

$\overbrace {3x-1} ^{\text{primer miembro}}=\overbrace {9+x} ^{\text{segundo miembro}}$

la variable

x

representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen las incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables (incógnitas) la hacen cierta.
Se llama solución de una ecuación a cualquier valor individual de dichas variables que la satisfaga. Para el caso dado, la solución es:

$x=5$

En el caso de que todo valor posible de la incógnita haga cumplir la igualdad, la expresión se llama identidad . Si en lugar de una igualdad se trata de una desigualdad entre dos expresiones matemáticas, se denominará inecuacion .

ejemplos

ecuaciones lineales o de primer grado

Las ecuaciones lineales o de primer grado son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.

Resolución de ecuaciones lineales

En general para resolver una ecuación lineal o de primer grado debemos seguir los siguientes pasos:

1º Quitar paréntesis.

2º Quitar denominadores.

3º Agrupar los términos en x en un miembro y los términos independientes en el otro.

4º Reducir los términos semejantes.

5º Despejar la incógnita.

Ejemplos de ecuaciones lineales

Despejamos la incógnita:

Agrupamos los términos semejantes y los independientes, y sumamos:

Quitamos paréntesis:

Agrupamos términos y sumamos:

Despejamos la incógnita:

Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.

Quitamos paréntesis, agrupamos y sumamos los términos semejantes:

Despejamos la incógnita:

Quitamos paréntesis y simplificamos:

Quitamos denominadores, agrupamos y sumamos los términos semejantes:

Quitamos corchete:

Quitamos paréntesis:

unidada # 3

numeros reales

inecuaciones

Inecuación de primer grado simple

Una inecuación es una expresión algebraica que consta de dos miembros separados por una desigualdad. La desigualdad puede ser < , ≤ , > , ≥.
Resolver una inecuación consiste en encontrar el valor o valores que la verifican, al contrario de las ecuaciones de primer grado, las inecuaciones tienen infinitas soluciones agrupadas en un conjunto.
El método de resolución de inecuaciones de primer grado se similar a la resolución de ecuaciones salvo por el hecho de que si multiplicamos los dos miembros de una inecuación por un número negativo cambia el sentido de la inecuación.
ejemplo

inecuacion de segundo grado

Una inecuación de segundo grado es una inecuación en donde encontramos números, una variable (que llamaremos

) que esta vez la podemos encontrar multiplicándose a ella misma, y un símbolo de desigualdad..

Ejemplo

Un ejemplo de inecuación de segundo grado podría ser:

donde podemos observar que el término

es el termino cuadrático, característico de las inecuaciones de segundo grado, ya que si éste no estuviera, tendríamos una inecuación de primer grado.

sucesiones

Definición

Se denomina sucesión a una función cuyo dominio es el conjunto de los números naturales.

Para denotar el n-ésimo elemento de la sucesión se escribe a_n en lugar de f(n).
Ejemplo:
a_n = 1/n
a₁ = 1, a₂ = 1/2, a₃ = 1/3, a₄ = 1/4, ...

Definición

Sucesión monótona creciente

Una sucesión es monótona creciente si se cumple que para todo n natural a_n <= a_n+1 (a₁ <= a₂ <= a₃ <= ... <= a_n).

Ejemplo:
a_n = n es monótona creciente.
a₁ = 1, a₂ = 2, a₃ = 3, a₄ = 4, ...

Definición

Sucesión monótona decreciente

Una sucesión es monótona decreciente si se cumple que para todo n natural a_n >= a_n+1 (a₁ >= a₂ >= a₃ >= ... >= a_n).

Ejemplo:
a_n = 1/n es monótona decreciente.
a₁ = 1, a₂ = 1/2, a₃ = 1/3, a₄ = 1/4, ...

A medida que aumenta n, los términos de la sucesión son cada vez más cercanos a 0. Si representamos los términos como puntos en una línea, esto significa que los puntos a_n se apiñan cada vez más cerca del punto 0 conforme n crece.
Sucesión con límite 0

Se dice que a_n tiende a 0, o que tiene límite 0.
Se expresa simbólicamente por: lim a_n = 0 o bien, ocasionalmente, por la notación abreviada a_n -> 0.

Definición

Límite finito

lim a_n = a <=> para todo ε>0 existe N natural / para todo n > N a - ε < a_n < a + ε, o lo que es lo mismo, |a_n - a| < ε.

Para cualquier número positivo ε, por pequeño que sea, podemos encontrar un natural N suficientemente grande tal que a partir del índice N en adelante se tiene que |a_n - a| < ε.
Es decir, si tomamos un entorno de a de cualquier radio siempre habrá un subíndice N tal que desde N en adelante todos los términos de la sucesión pertenecen a dicho entorno.

Límite infinito de una sucesión

Consideremos la sucesión a_n = n².
a₁ = 1
a₂ = 4
a₃ = 9
a₄ = 16
...
a₁₀ = 100
...
a₁₀₀ = 10.000

Al crecer n, a_n no tiende a un límite definido, sino que crece más allá de toda cota. Se dice que a_n tiende a infinito.

Definición

Convergencia y divergencia

Cuando una sucesión tiene límite finito a se dice que es convergente y converge a a.
Una sucesión que tiene límite infinito se llama divergente.
Una sucesión que carece de límite se llama oscilante.

La sucesión a_n = 1/n converge a 0.
La sucesión a_n = n² es divergente.
La sucesión a_n = sen n es oscilante, pues sus valores varían entre 1 y -1.
b > c.

natural / para todo n > n₂ c - ε < a_n < c + ε Consideremos un ε tal que c+ε < b-ε, o sea ε < (b - c)/2

Sea N = max {n₁,n₂}
Para todo n > N se cumple

b - ε < a_n < b + ε
c - ε < a_n < c + ε

Absurdo, pues a_n no puede pertenecer a dos entornos disjuntos.
Absurdo de suponer b ≠ c.
Por lo tanto b = c.

numeros reales

relacion de orden

Una ecuación es un enunciado matemático que tiene dos expresiones separadas por un signo igual. La _expresión a la izquierda del signo igual tiene el mismo valor que la _expresión a la derecha.

Una o ambas expresiones pueden contener variables. Resolver una ecuación implica trabajar con las expresiones y encontrar el valor de las variables.

Ejemplo:

Resolver la ecuación: 7x = 21

Para que la ecuación se mantenga igual, debes aplicar la misma operación a ambos lados de la ecuación. Si multiplicamos (o dividimos)un lado por una cantidad, debemos multiplicar (o dividir) el otro lado por la misma cantidad.

Esta ecuación se puede resolver dividiendo ambos lados por 7.

La ecuación sería 7x/7 = 21/7. Esto se puede simplificar a x = 21/7 o x = 3.

Puedes verificar tu cálculo sustituyendo el valor de x en la ecuación original. (7*3=21).

Ejemplo 2

Una ecuación de segundo grado es toda expresión de la forma:

ax² + bx +c = 0 con a ≠ 0.

Se resuelve mediante la siguiente fórmula:

ejemplos

Por factorización

Este método consiste en resolver la ecuación como un producto de binomios, es decir encontrar dos números que multiplicados den como resultado “c” y sumados den “b”.

Este método se usa cuando a = 1.

Ejemplo:

x² + 3x – 18 = 0

Buscamos dos números que multiplicados den -18 y sumados 3, y nos encontramos con que el 6 y el -3 cumplen con estos requisitos…. 6 · (-3) = -18 y 6 + (-3) = 3

(x + 6)(x – 3) = 0

INECUACIONES

Una inecuación es una expresión de la forma: f(x) < g(x), f(x) <= g(x), f(x) > g(x) o f(x)>= g(x).

La resolución de las inecuaciones es muy parecida a la resolución de las ecuaciones.

5x + 6 < 3x - 8
5x - 3x < -8 - 6
2x < -14
x < -7

Todos los valores de x menores que -7 satisfacen la inecuación.

Es muy importante tener en cuenta que si multiplicamos por un numero negativo una inecuación tenemos que cambiar el signo de la desigualdad.

3x > -2
-9x < 6
x < -2/3
Sistemas de inecuaciones de primer grado con una incógnita.

lunes, 3 de julio de 2017

unidad numero 3 numeros reales

Ejemplos de números irracionales

Números Racionales

Ejemplos de números racionales

Números complejos

Ejemplos:

Operaciones con conjuntos

Propiedades

Términos:

2.- Monomios:

3.- Trinomios:

4.- Polinomios (más de tres términos):

Sustracción de monomios

Multiplicación de monomios

División de monomios

Potencia de monomios

Multiplicación de fracciones

Multiplicación de una fraccion con un número natural

Multiplicación de dos fracciones

Multiplicación de fracciones inversas

Otras operaciones con fracciones

Potenciacion de fracciones

Radicación de fracciones

Racionalización

Cálculo del máimo común divisor y mínimo común múltiple

Suma o adición

Propiedades de la suma:

Resta o substración

Propiedades de la resta:

Producto o multiplicación

División

Propiedades de la division

Potenciación

Propiedades de la potenciación:

Radicación

Ejemplos de razones

Ejemplos de proporciones:

Proporción directa:

Proporción inversa:

Definición de valor absoluto

Resolución de ecuaciones lineales

Ejemplos de ecuaciones lineales

Inecuación de primer grado simple

Definición

Definición

Sucesión monótona creciente

Definición

Sucesión monótona decreciente

Definición

Límite finito

Límite infinito de una sucesión

Definición

Convergencia y divergencia

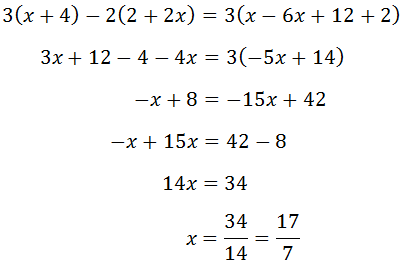
No hay comentarios:

Publicar un comentario

videos relacionados a las unidades