conjuntos

unidad # 2

conjuntos 

Definicion , tipos de cardinalidad  

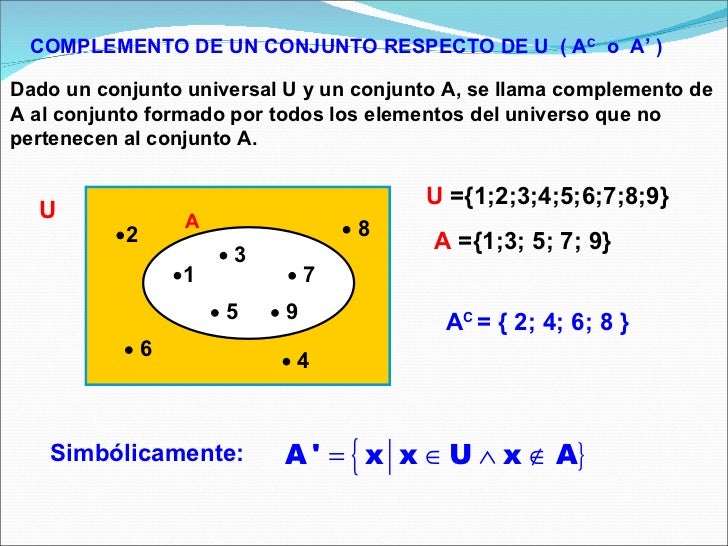
Conjunto Universal

Con el ánimo de evitar confusiones, cuando definimos un conjunto debemos especificar de donde se están tomando los elementos que lo conforman.  Esto significa que debe existir una base de la cual tomamos los elementos, esta base sobre el cual trabajamos es llamada conjunto universal  Usaremos siempre la letra U para representar el conjunto universal. 

  

Por ejemplo, si quieres definir B como el conjunto conformado por las vocales a e i, el conjunto universal podría ser el conjunto de las vocales.  En la figura anterior se muestra cómo puedes usar los diagramas de Venn para representar la relación entre el conjunto B y su conjunto universal U.
Observa que el conjunto universal puede tener exactamente los elementos de los conjuntos que abarca o más.

Conjunto vacío

Consideremos la existencia de un conjunto que no tiene elementos, este es llamado conjunto vacío.

Para representar dicho conjunto usamos el reconocido símbolo del vacío, como se muestra en la imagen de la derecha.
También, haciendo uso de la descripcion por extencion  representamos el conjunto vacío por medio de los corchetes {}.    Como el conjunto vacío no tiene elementos, no podemos ubicar ningún elemento en el interior de los corchetes. 

Conjuntos unitarios

El conjunto unitario se distingue por tener solo un elemento.  No importa qué tipo de elemento tenga el conjunto, un gato, un perro, un número, una letra, o cualquier otra cosa, si tiene un solo elemento es llamado conjunto unitario.

Conjuntos finitos

Este tipo de conjunto también se distingue por la cantidad de elementos que posee.  Un conjunto es finito si podemos contar la cantidad de elementos que lo conforman.
Por ejemplo, el conjunto de las letras del idioma castellano es finito porque en total son 27 letras.  En la imagen de la derecha se muestran otros conjuntos finitos.  Te puedes dar cuenta que los conjuntos unitarios también son finitos. 

Conjuntos infinitos

No es fácil encontrar en la naturaleza ejemplos de este tipo de conjuntos.  Los conjuntos infinitos son aquellos a los cuales no les podemos contar la cantidad de elementos que los componen.  El método más fácil para representar este tipo de conjuntos es por comprencion .  Basta con mencionar las características que tienen en común los elementos del conjunto y los estaremos determinando a todos.  Considera el conjunto de los números que terminan en tres, podríamos definirlo así:  Sea T={x∣x es número y termina en tres}.
También existe una manera de representar algunos conjuntos infinitos por extencion .  Basta exhibir los primeros elementos del conjunto e indicar con puntos suspensivos que la lista continua indefinidamente.  En el caso del conjunto T, definido en el párrafo anterior y conformado por los números que terminan en tres, se tiene T={3, 13, 23, 33, 43, 53, ...}. 

Los ejemplos más sencillos y comunes de conjuntos infinitos los encontramos en los números.  ¿Cuántos números pares hay? ¿cuántos múltiplos tiene el tres?  Estos conjuntos son infinitos, y no es porque este más allá de nuestra capacidad contar la cantidad de elementos que tienen.  Es que es imposible hacerlo porque no hay un número que represente la cantidad de elementos que el conjunto contiene.

No debes confundir los conjuntos infinitos con conjuntos finitos que tienen una gran cantidad de elementos.  Por ejemplo, ¿consideras el conjunto de todos los granos de arena en el planeta Tierra, un conjunto infinito?  En este caso, aunque el conjunto tenga una gran cantidad de elementos debe existir un número que la represente, así sea muy grande. 

Conjuntos Coordinables o equipotentes

Se dice que dos conjuntos son coordinables o equipotentes cuando están formados por el mismo número de elementos .   Para que tengas un ejemplo, supón que en una fiesta de cumpleaños existen la misma cantidad de copas de vino como de invitados:

La manera correcta de establecer si dos conjuntos son coordinables o no, es estableciendo una relación entre sus elementos.  Esta relación debe tener unas características especiales que te explicamos a continuación:  
ejemplo:

Relaciones uno a uno

 

Podemos establecer la siguiente correspondencia entre los conjuntos:

Como te puedes dar cuenta, la primera condición no se cumplió, pues cada elemento del conjunto invitados debe estar relacionado con un único elemento del conjunto copas.  En este caso eso no cierto, ya que existe una persona que no está relacionada con ninguna copa.  Los conjuntos no son coordinables ahora.
Si tratamos de arreglar las cosas relacionando la persona que acaba de llegar con unas de las copas obtendremos la siguiente relación.

Nota que ahora la condición que no se cumple es la segunda, ya que cada elemento del conjunto copas, debe estar relacionado con un único elemento del conjunto invitados y en este caso eso no es cierto, pues hay una copa que está relacionada con dos personas.
Verifica lo que aprendiste con el siguiente interactivo:

Relaciones entre conjuntos y elementos

Para comprender las relaciones entre los conjuntos, debes comprender primero como se relacionan estos con los elementos}

Relación de pertenencia

Para comenzar, debes comprender la relación entre los  conjuntos y los elementos  que lo conforman.  Cuando un objeto es uno de los elementos de un conjunto decimos que pertenece al conjunto.
Como has visto, es posible representar gráficamente la relación de pertenencia por medio de diagramas de evven dibujando el elemento dentro de un circulo que representa el conjunto.  Ahora aprenderás a representar esta relación por medio de símbolos matemáticos.

Se usa el símbolo que se muestra en la figura de la izquierda como el símbolo de la pertenencia.  Si queremos representar que cierto objeto no pertenece a determinado conjunto usaremos el mismo símbolo atravesado por una línea, como se muestra en la figura de la derecha.  Veamos como debe ser usado este símbolo:

Relación de contenencia y subconjuntos

Definamos como `F` y `G` los conjuntos que se muestran en el siguiente diagrama de evven:

Como te puedes dar cuenta, cada elemento que pertenece al conjunto `G`, pertenece también al conjunto `F`.  Cuando se da esta situación decimos que un  conjunto está contenido en el otro, o que es un subconjunto del otro.
En este caso `G` está contenido en `F`, o lo que es igual, `G` es subconjunto de `F`.

La manera correcta de representar la relación de contenencia es dibujar un conjunto dentro del otro.  Para el caso de los conjuntos `F` y `G` definidos anteriormente, la representación correcta es como se muestra en la figura de abajo.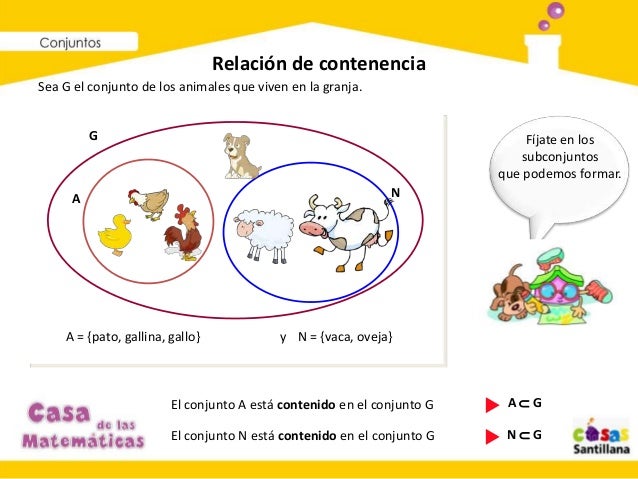

Se dice que dos conjuntos son iguales si tienen exactamente los mismos elementos.  Una forma práctica de establecer si dos conjuntos son iguales es determinar si se contienen el uno al otro.

Por ejemplo, para verificar si los conjuntos `K` y `L` de la imagen son iguales debemos verificar si  `K sube L` y además `L sube K`.

Fíjate que no importó que algunos elementos estuvieran repetidos, o en que orden estuvieran presentados los elementos.  Resultaría igual escribir por ejemplo `{p,q,r,q,s,r,p}` que  `{r,s,p,q}` o que `{p,r,q,s}`, es decir: `{p,q,r,q,s,r,p}={r,s,p,q}={p,r,q,s}`.
Si se da el caso que dos conjuntos no son iguales usamos el símbolo `!=`.  De esta manera la expresión `A!=B` debe ser leída como “`A` es diferente a `B`”, o “`A` y `B` no son iguales”.

Relación de igualdad

Veremos ahora en que condiciones podemos decir que dos conjuntos son iguales, esto lo haremos a través de la relación de igualdad entre conjuntos.

Observa los conjuntos  `K` y `L` definidos así: `K={p,q,r,q,s,r,p}` y `L={s,r,p,q}`.

Se dice que dos conjuntos son iguales si tienen exactamente los mismos elementos.  Una forma práctica de establecer si dos conjuntos son iguales es determinar si se contienen bemos verificar si  `K sube L` y además `L sube K`.

.

todos los elementos  que no importó que algunos elementos estuvieran repetidos, o en que orden estuvieran presentados los elementos.  Resultaría igual escribir por ejemplo `{p,q,r,q,s,r,p}` que  `{r,s,p,q}` o que `{p,r,q,s}`, es decir: `{p,q,r,q,s,r,p}={r,s,p,q}={p,r,q,s}`.
Si se da el caso que dos conjuntos no son iguales usamos el símbolo `!=`.  De esta manera la expresión `A!=B` debe ser leída como “`A` es diferente a `B`”, o “`A` y `B` no son iguales”.

Operaciones entre conjuntos

Además de relacionar los conjuntos a través de la contenecia  y la igualdad , podemos crear unos nuevos a través de las operaciones entre conjuntos.  Aquí aprenderás de que se trata.

Unión de conjuntos

Supongamos que tenemos los conjuntos `a y b definidos como se muestra en la siguiente figura:

Podemos crear otro conjunto conformado con los elementos  que pertenezcan a `a y b`.  A este nuevo conjunto le llamamos unión de a y b `, y lo notamos de la siguiente manera: `B A.  En la imagen de abajo puedes observar el resultado de unir los conjuntos `M` y `N`.

Al elegir qué elementos estarán en la unión de nuestros conjuntos `a y b , debes preguntarte cuáles están en el conjunto `A` “o” en el conjunto B.  El resultado de la operación será el conjunto conformado por todos los elementos del conjunto universal `U`, que cumplan la condición de estar en uno o en otro.  


 

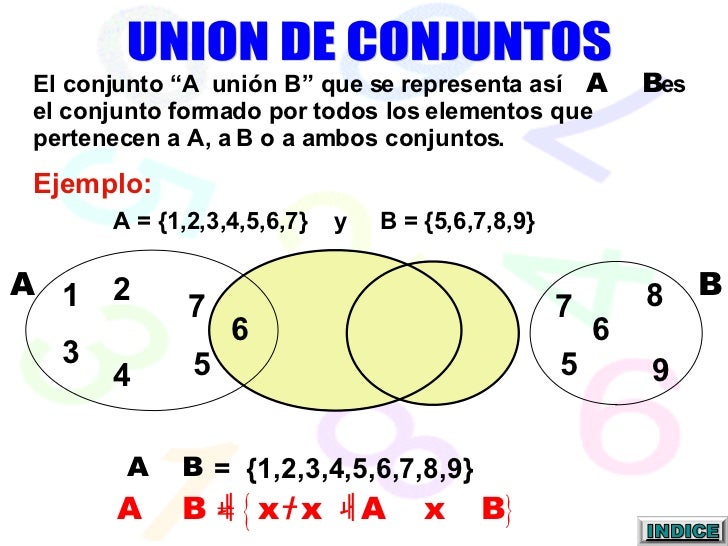
Tenemos en este caso: `M uu N={a,c,b,g,e,1}.`

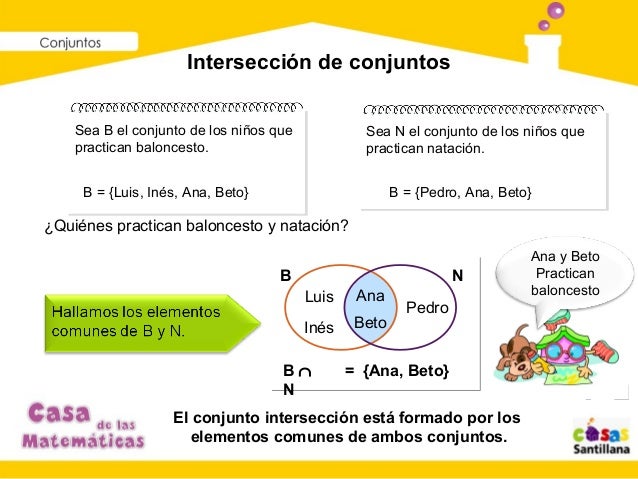
Intersección de conjuntos

Sigamos tomando como ejemplo los conjuntos `M` y `N` definidos anteriormente.  Podemos determinar un nuevo conjunto conformado por los elementos que nuestros conjuntos `M` y `N` tienen en común.  A este nuevo conjunto le llamamos intersección de `M` y `N` y lo notamos de la siguiente manera: `M nn N`.

Para determinar que elementos pertenecen a la intersección de los conjuntos `M` y `N` te puedes preguntar qué elementos están en `M` “y” en  `N`.  Todos los elementos del conjunto `U` que cumplan esta condición deberán estar en el conjunto `M nn N`.  En la figura de la arriba podemos ver la intersección de nuestros conjuntos `M` y `N`, tenemos que `M nn N = {b}`.


 

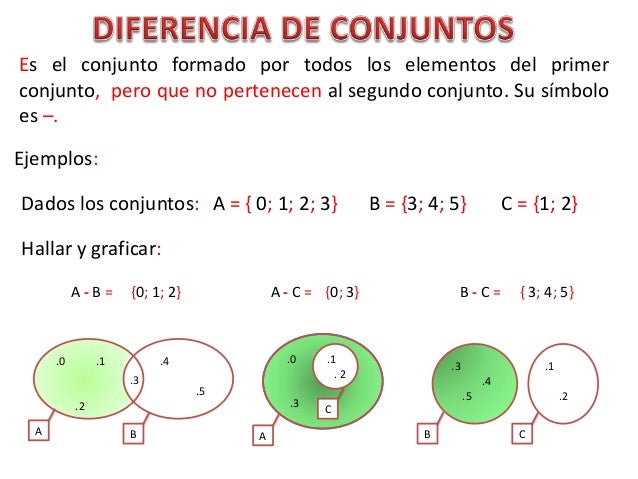
Diferencia de conjuntos

Además de la unión y la intersección podemos realizar la diferencia de conjuntos.

En este caso se deben seleccionar los elementos de un conjunto que no estén en el otro.  Por ejemplo, si realizas la operación `M` menos `N`, debes seleccionar los elementos de `M` que no están en `N`.  Representamos la diferencia M menos N así: `M  \\  N`.  Observa que en este caso `M  \\  N={a,c}`.


 

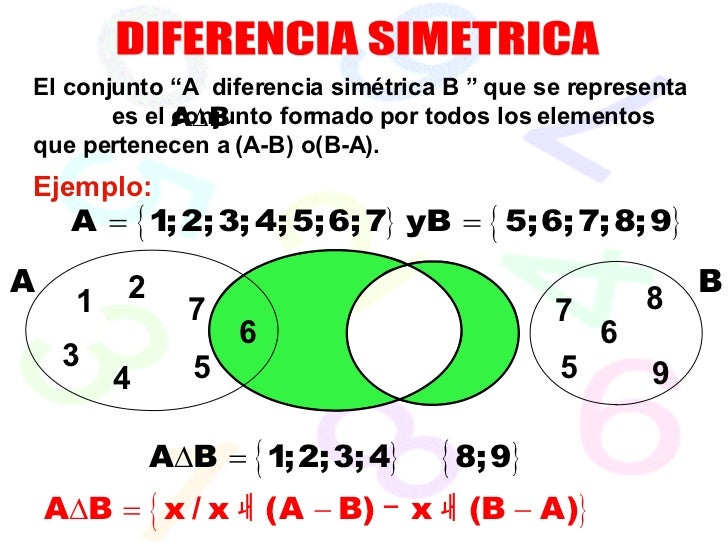
Diferencia simétrica de conjuntos

Que el nombre esta operación no te alarme, también es muy sencilla. 

En esta ocasión se deben escoger los elementos de `M` que no están en `N`, y los elementos de `N` que no están en `M`.  Puedes ver el resultado de la diferencia simétrica entre `M` y `N` en la figura de la izquierda.  Representamos la diferencia simétrica a través del símbolo `Delta`.  En el caso de nuestros conjuntos `M` y `N` tenemos: `M  Delta  N={a,c,g,1,e}`.

Complemento de un conjunto

La ultima operación que estudiaremos no es entre dos conjuntos.  Decimos que el complemento de `M` es el conjunto conformado por todos los elementos del conjunto universal `U`, que no pertenecen al conjunto `M`.  Es común usar los símbolos `M^c`, `bar(M)` o `M'` para representar el complemento del conjunto `M`, nosotros usaremos el símbolo `M^c`.  En nuestro caso tenemos `M^c ={j,f,g,1,e,i,h}` y `N^c={i,h,j,f,a,c}`.

Problemas que se pueden resolver con conjuntos

Es posible usar los conceptos aprendidos para interpretar y resolver cierto tipo de problemas, aprende cómo hacerlo.

Observa la siguiente situación: en un salón de clases de `50` niños y niñas, a `10` les gusta solo el helado de fresa y a `5` solo el helado de chocolate.  Si a `20` niños no les gusta el helado ni de fresa ni de chocolate: ¿a cuántos niños les gustan los dos helados?, ¿a cuántos niños les gusta en total el helado de fresa?, ¿a cuántos el de chocolate?
¡Mira la solución, es más sencilla de lo que crees!  Primero representaremos la situación con diagramas de evven llamaremos `F` al conjunto de los estudiantes a los que les gusta el helado de fresa y `C` al de conjunto de niños que gustan del helado de chocolate.

Estos dos conjuntos deben estar contenidos en unconjunto universal que es precisamente el salón de clase completo.  Por lo tanto podemos representar toda la situación a través del siguiente diagrama.

Las diferentes regiones del diagrama representan diferentes grupos de estudiantes.

   

                                          interseccion

Por ejemplo, en la interseccion de los conjuntos `F` y `C` se representa la población de estudiantes que gustan de los dos helados, mientras que la región exterior a los conjuntos, representa la parte del curso que no gusta de ninguno.  Podemos por lo tanto ubicar las cantidades de estudiantes en las zonas correspondientes: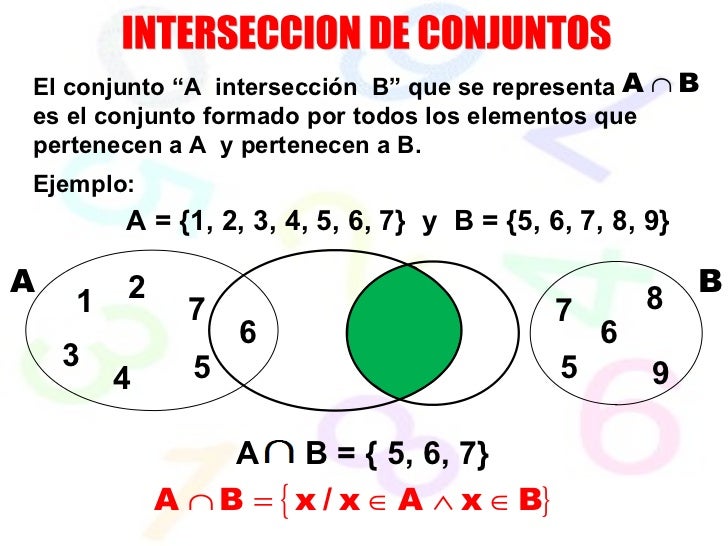 

Observa que el `10` y el `5` quedaron ubicados en zonas que comprenden los estudiantes que gustan de solo de uno de los dos helados, por su parte el `20` está ubicado por fuera de los dos conjuntos, representando los estudiantes que no gustan de estos sabores de helado, tal y como lo dice el enunciado del problema.  Ahora bien, tenemos `10` estudiantes que solo gustan del helado de fresa, `5` solo el de chocolate y `20` ninguno de los dos, lo que nos da un total de `10+5+20=35.`

Como el curso completo se compone de `50` estudiantes tenemos un faltante de `50-35=15.`  ¿A qué grupo pertenecen estos `15` estudiantes?

Solo hay una opción: a la región que gusta de los dos helados, es decir la intersección de los conjuntos `F` y `C.`

Podemos entonces responder todas las preguntas hechas inicialmente: a `15` niños les gustan los dos helados, en total a `25` les gusta el helado de fresa y a `20` les gusta el helado de chocolate.
Una última pregunta: ¿a cuántos estudiantes les gusta el helado de fresa o el de chocolate?
Recuerda que la union  de conjuntos está conformada por los elementos que pertenecen a uno u otro, por lo tanto la respuesta es la cantidad de estudiantes de la unión `FuuC.`  Esto quiere decir que a  `30` estudiantes les gusta el helado de fresa o el de chocolate.

  

cuantificadores  

Cuando se habla de cuantificadores en términos de Lógica, Teoría de Conjuntos o Matemáticas en general, se hace referencia a aquellos símbolos que se utilizan para indicar cantidad en una proposición, es decir, permiten establecer “cuántos” elementos de un conjunto determinado, cumplen con cierta propiedad.

Los cuantificadores permiten la construcción de proposiciones a partir de funciones proposicionales, bien sea particularizando o generalizando. Por ejemplo, si consideramos la función proposicional:

P(x) = x es menor que dos

Esto podría particularizarse así: “Existe un número real que es menor que dos” o generalizarlo diciendo: “Todos los números reales son menores que dos”.

En cualquiera de los dos casos, se especifica un conjunto donde está tomando valores la variable, para nuestro ejemplo, el conjunto de los números reales.

Para notar la particularización y la generalización, se utiliza la siguiente simbología, respectivamente:


que se lee: “existe un equis que pertenece a erre (a los reales), tal que equis es menor que dos”

Mientras que

se lee: “para todo equis que pertenece a erre (a los reales), se cumple que equis es menor que dos”

El símbolo (para todo…) se denomina cuantificador universal, y el símbolo (existe al menos un…) se denomina cuantificador existencial.

Así, un cuantificador transforma una función proposicional, en una proposición a la cual se le asigna un valor de verdad.

Los cuantificadores más utilizados son entonces:

• CUANTIFICADOR UNIVERSAL 
•  (para todo…): se utiliza para afirmar que TODOS los elementos de un conjunto, cumplen con una condición o propiedad determinada. Esto se expresa como:

• CUANTIFICADOR EXISTENCIAL (existe al menos un…): se utiliza para indicar que existen uno o más elementos en el conjunto A que cumple(n) con una condición o propiedad determinada.

• CUANTIFICADOR EXISTENCIAL ÚNICO (existe un único…): se utiliza para indicar que existe exactamente un elemento en el conjunto A que cumple con una condición o propiedad determinada.

NEGACIÓN DE PROPOSICIONES CON CUANTIFICADORES

Sea p(x) una función proposicional con extensión A, entonces:

operaciones entre conjuntos 

En las matematicas  podemos definir a un conjunto como una colección desordenada de objetos, los objetos de un conjunto pueden ser cualquier cosa siempre que tengan una relación entre ellos, a los objetos de un conjunto de les llama elementos o miembros  de dicho conjunto, por lo tanto un conjunto contiene a sus elementos  Se representan con una letra mayúscula y a los elementos o miembros de ese conjunto se les mete entre llaves ({,}).
Dos conjuntos  se pueden combinar de muchas maneras distintas, por ejemplo, teniendo un conjunto de la gente que juega al fútbol y otro de la gente que juega a baloncesto podemos hacer muchas combinaciones como el conjunto de personas que juegan a fútbol o baloncesto, las que juegan a fútbol y baloncesto, las que no juegan a baloncesto, etc.
Por lo tanto vamos a ver las distintas operaciones que hay en los conjuntos:


Unión



  diagrama de evenn de la unión de dos  conjuntos  A ∪ B
El símbolo de esta operación es: ∪.
Sean A y B dos conjuntos, la union de ambos (A ∪ B) es el conjunto C el cual contiene a todos los elementos pertenecientes alconjunto A y al conjunto B.
Un elemento x pertenece a la unión de los conjuntos A y B si, y sólo si, x pertenece al conjunto A o x pertenece al conjunto B, por lo tanto ${\displaystyle A\cup B=\{x/x\in A\lor x\in B\}}$


Ejemplos

En el diagrama de evenn  que se muestra en la imagen de la derecha se puede observar como es de forma gráfica, a continuación pondré también algunos ejemplos prácticos:

1. Ejemplo: La unión de los conjuntos A={1,2,3} y B={2,4,6} sería el conjunto C={1,2,3,4,6}, esto es: {1,2,3}∪{2,4,6}={1,2,3,4,6}
2. Ejemplo: La unión de personas que juegan al fútbol y de personas que juegan al baloncesto serían las personas que juegan a fútbol o baloncesto.

Intersección



  diagrama de evven que muestra la interseccion  de dos conjuntos  A ∩ B
El símbolo de esta operación es: ∩.
Sean A y B dos conjuntos, la interseccion  de ambos (A ∩ B) es el conjunto C el cual contiene los elementos que están en A y que están en B.
Un elemento x pertenece a la intersección de los conjuntos A y B si, y sólo si, x pertenece al conjunto A y x pertenece al conjunto B, por lo tanto 





${\displaystyle }$
${\displaystyle A\cap B=\{x/x\in A\land x\in B\}}$


Ejemplos

En el Diagrama de Venn que se muestra en la imagen de la derecha se puede observar como es de forma gráfica, a continuación pondré también algunos ejemplos prácticos:

1. Ejemplo: La intersección de los conjuntos A={1,2,3} y B={2,4,6} sería el conjunto C={2}, esto es: {1,2,3}∩{2,4,6}={2}
2. Ejemplo: La intersección del conjunto de números pares y el conjunto de números impares sería el conjunto C={${\displaystyle \emptyset }$} o sea no sería ningún número. Por lo tanto se dice que estos dos conjuntos son disjuntos
3. Ejemplo: La intersección de personas que juegan al fútbol y de personas que juegan al baloncesto serían las personas que juegan a fútbol y a baloncesto a la vez.

Disjuntividad

Se dice que dos conjuntos A y B son disjuntos  cuando la interseccion  de ambos es el conjunto vacio A ∩ B= {${\displaystyle \emptyset }$

Ejemplos

1. Ejemplo: La intersección del conjunto de números pares y el conjunto de números impares sería el conjunto C={${\displaystyle \emptyset }$} o sea serían disjuntos.
2. Ejemplo: La intersección del conjunto de personas que juegan a baloncesto y el conjunto de personas que juegan a fútbol es el conjunto vacío, osea serían disjuntos.
3. Ejemplo: La intersección de A={3,7,8} y B={1,2,9} sería C={${\displaystyle \emptyset }$}, ya que {3,7,8}∩{1,2,9}={${\displaystyle \emptyset }$} por lo tanto A y B son disuntos.

 



  diagrama de even que muestra la diferncia  de dos conjuntos A \ B
El símbolo de esta operación es: \.
La diferencia consiste en eliminar de A todo elemento que esté en B, también se puede denotar con el símbolo de la resta A-B, por lo tanto, la diferencia de los conjuntos A y B es el conjunto C que tiene a todos los elementos que están en A, pero no en B.
También se le puede llamar a la diferencia de A y B: complementario de B con respecto a A.
Por lo tanto, un elemento pertenece a la diferencia de A y B si, y sólo si ${\displaystyle \{x/x\in A\land x\not \in B\}}$


Ejemplos

1. Ejemplo: La diferencia simétrica del conjunto A={1,2,3,4,5,6} y B={4,5,6,7,8,9} es el conjunto C={1,2,3,7,8,9}, matemáticamente: {1,2,3,4,5,6} Δ {4,5,6,7,8,9}={1,2,3,7,8,9}
2. Ejemplo: La diferencia simétrica del conjunto de personas que juegan a fútbol y el conjunto de personas que juegan a baloncesto es el conjunto de personas que juegan sólo a fútbol y sólo a baloncesto, pero no que jueguen a ambos a la vez. 

Complemento



  diagrama de even que muestra el complemento  de un conjunto  A
El símbolo de esta operación es: A^∁, o también se suele representar con el símbolo A
Supongamos que U es el conjunto universal, en el cual se encuentran todos los elementos posibles, entonces el complementario de A con respecto a U se consigue restando a U todos los elementos de A. A=U-A
Por lo tanto, un elemento pertenece al complementario de A si, y sólo si ${\displaystyle A^{c}=\{x/x\in U\land x\not \in A\}}$


Ejemplos

1. Ejemplo: El complementario del conjunto de números pares es el conjunto de números impares.
2. Ejemplo: El complementario del conjunto de personas que juegan a fútbol es el conjunto de personas que no lo juegan.
3. Ejemplo: El conjunto de todos los números positivos mayores de 5, incluyendo el 5, es el conjunto {1,2,3,4}

Diferencia simétrica



diagrama de even que muestra la diferencia simetrica  de dos conjuntos  A Δ B
El símbolo de esta operación es: Δ.
La diferencia simétrica de dos conjuntos A y B es otro conjunto el cuál posee los elementos que o bien se encuentran en A, o bien se encuentran en B, pero no en los dos a la vez. A Δ B = C, donde C no tiene elementos que estén en A y en B a la vez.
Por lo tanto, un elemento pertenece a la diferencia simétrica de A y B si, y sólo si: ${\displaystyle A}$Δ${\displaystyle B=\{x/x\in A\land x\not \in B\lor x\not \in A\land x\in B\}}$


Ejemplos

1. Ejemplo: La diferencia simétrica del conjunto A={1,2,3,4,5,6} y B={4,5,6,7,8,9} es el conjunto C={1,2,3,7,8,9}, matemáticamente: {1,2,3,4,5,6} Δ {4,5,6,7,8,9}={1,2,3,7,8,9}
2. Ejemplo: La diferencia simétrica del conjunto de personas que juegan a fútbol y el conjunto de personas que juegan a baloncesto es el conjunto de personas que juegan sólo a fútbol y sólo a baloncesto, pero no que jueguen a ambos a la vez.

Producto cartesiano

En un conjunto los elementos están desordenados y el orden es muy importante, por ello necesitamos algún tipo de estructura diferente para representar a los elementos ordenados, de ahí salen las n-tuplas ordenadas.
La n-tupla ordenada ${\displaystyle (a_{1},a_{2},a_{3},\dots ,a_{n})}$ es la colección ordenada dónde su primer elemento es ${\displaystyle (a_{1})}$, ${\displaystyle (a_{2})}$ es su segundo elemento, ... y ${\displaystyle (a_{n})}$ el elemento n-ésimo.
Se puede decir que dos n-tuplas ordenadas son iguales si, y sólo si, cada elemento numerado de cada par es igual, osea, ${\displaystyle (a_{1},a_{2},a_{3},\dots ,a_{n})}$ = ${\displaystyle (b_{1},b_{2},b_{3},\dots ,b_{n})}$ esto sucede si, y sólo si ${\displaystyle (a_{i})}$=${\displaystyle (b_{i})}$ para i= 1,2,3,...,n. Las 2-tuplas se llaman pares ordenados (a,b) y (c,d), estos son iguales si, y sólo si a=c y b=d.
Ahora haciendo referencia al producto cartesiano de dos conjuntos:
El símbolo de esta operación es: ×
El producto cartesiano de dos conjuntos A y B es el conjunto C, C = A × B, donde los pares ordenados (a,b) están formados por un primer elemento perteneciente a A y un segundo elemento perteneciente a B.
${\displaystyle A}$×${\displaystyle B=\{(a,b)/a\in A\land b\in B\}}$


Ejemplos

1. Ejemplo: El producto cartesiano de A={2,3} y B={a,b,c} es A×B={(2,a),(2,b),(2,c),(3,a),(3,b),(3,c)}

Principio de inclusión-exclusión

Es la generalización del resultado de las uniones de un número arbitrario de conjuntos, es una técnica muy importante que se usa principalmente en los problemas de enumeración.

Sucede por ejemplo cuando queremos encontrar un cardinal de la unión de dos conjuntos y para encontrar dicho número de la unión de dos conjuntos finitos A y B, hay que tener encuenta que en A∪B cada elemento de A está solo una vez en A, pero no en B, y viceversa, pero hay algunos elementos que pueden pertenecer a A y a B a la vez, por lo tanto el principio  de  inclusion _ exclusion se basa en restar a la unión de dos conjuntos finitos la intersección de ambos.
Matemáticamente: A∪B - A∩B


Identidad

En matematicas, una identidad  es cuando dos objetos que aparentemente son distintos por la forma en la que se representan, al final son lo mismo. Por lo tanto, una identidad  es una igualdad  entre dos expresiones, entre los conjuntos existen una serie de leyes de identidades, que les muestro a continuación:


Leyes de identidad

• A ∪ ${\displaystyle \emptyset }$ = A, la unión de un conjunto cualquiera con el conjunto vacío es el mismo conjunto.
• A ∩ U = A, la intersección de un conjunto cualquiera con el conjunto universal es el mismo conjunto.

Leyes de dominación

• A ∪ U = U, la unión de un conjunto cualquiera con el conjunto universal, es el conjunto universal.
• A ∩ ${\displaystyle \emptyset }$ = ${\displaystyle \emptyset }$, la intersección de un conjunto cualquiera con el conjunto vacío, es el conjunto vacío.

Leyes idempotentes

• A ∪ A = A, la unión de un conjunto cualquiera consigo mismo, es el mismo conjunto.
• A ∩ A = A, la intersección de un conjunto cualquiera consigo mismo, es el mismo conjunto.

Ley de complementación

• A, la negación de la negación de un conjunto cualquiera, es el mismo conjunto.

Leyes conmutativas

• A ∪ B = B ∪ A
• A ∩ B = B ∩ A

Leyes asociativas

• A ∪ (B∪C) = (A∪B) ∪ C
• A ∩ (B∩C) = (A∩B) ∩ C

Leyes distributivas

• A ∩ (B∪C) = (A∩B) ∪ (A∩C)
• A ∪ (B∩C) = (A∪B) ∩ (A∪C)

Leyes de De Morgan



Representación gráfica de las leyes de De Morgan
• A ∪ B = A ∩ B
• A ∩ B = A ∪ B
La forma generalizada es:


${\displaystyle {\overline {\bigcap _{i\in I}A_{i}}}\equiv \bigcup _{i\in I}{\overline {A_{i}}}}$

${\displaystyle {\overline {\bigcup _{i\in I}A_{i}}}\equiv \bigcap _{i\in I}{\overline {A_{i}}}}$

donde I es un conjunto indexado, posiblemente incontable.


Leyes de absorción

• A ∪ (A∩B) = A
• A ∩ (A∪B) = A

Leyes de complemento

• A ∪ A = U, la unión de un conjunto cualquiera con su complementario, es el conjunto universal.
• A ∩ A = ${\displaystyle \emptyset }$, la intersección de un conjunto cualquiera con su complementario, es el conjunto vacío.

Uniones e intersecciones generalizadas

Las operaciones de unión y de intersección tienen la
propiedad asociativa por lo tanto si tenemos tres conjuntos A, B y C...
La unión de esos tres conjuntos es otro conjunto D el cuál contiene todos aquellos elementos que están al menos en uno de los conjuntos A, B o C. (A∪B∪C)
Un elemento x pertenece a la unión de los conjuntos A, B y C si, y sólo si, x pertenece al conjunto A o x pertenece al conjunto B o x pertenece al conjunto C, por lo tanto: ${\displaystyle A\cup B\cup C=\{x/x\in A\lor x\in B\lor x\in C\}}$
La intersección de los conjuntos A, B y C queda como resultado otro conjunto D el cuál tiene los elementos que están estrictamente en A, en B y en C. (A∩B∩C)
Un elemento x pertenece a la intersección de los conjuntos A, B y C si, y sólo si, x pertenece al conjunto A, x pertenece al conjunto B y x pertenece al conjunto C, por lo tanto: ${\displaystyle A\cap B\cap C=\{x/x\in A\land x\in B\land x\in C\}}$


Ejemplos

1. Ejemplo: La unión del conjunto de personas que juegan al fútbol, el conjunto de personas que juegan al baloncesto y el conjunto de personas que juegan a tenis, es el conjunto de personas que juegan a uno o más de los tres deportes citados; sin embargo, la intersección de esos tres conjuntos sería el conjunto de personas que juegan a los tres deportes.
2. Ejemplo: Sea A={2,4,6,20}, B={1,7,13,20} y C={0,5,20}, la unión de A, B y C es el conjunto D={0,1,2,4,5,6,7,13,20} y la intersección de A, B y C es el conjunto D={2

relaciones  de conjuntos 

Definición matemática de Relación y de Función

 

En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio , con un segundo conjunto, llamado Recorrido o Rango , de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.
Por su parte, una  funcion  es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
De las definiciones anteriores podemos deducir que todas las funciones son relaciones , pero no todas las relaciones son funciones.
También debemos agregar que toda ecuación es una Relación , pero no toda ecuación es una Función

Todas las Relaciones pueden ser graficadas en el Plano Cartesiano

El plano cartesiano está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen .

Dos ejes perpendiculares entre sí.

El plano carteciano  tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas pares ordenadas .
El dominio de una relación es el conjunto de preimágenes ; es decir, el conjunto formado por los elementos del conjunto de partida que están relacionados. Al conjunto de imágenes , esto es, elementos del conjunto de llegada que están relacionados, se le denomina recorrido o rango .
Ejemplo 3
Sea A = {1, 2, 3, 4}  y B = {4, 5, 6, 7, 8} y R la relación definida de A en B determinada por la regla “ y es el doble de x ” o  “ y = 2 x ”, encontrar dominio y rango de la relación.
Solución
El total de pares ordenados que podemos formar, o producto cartesiano es:
A x B =  {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8)}
Pero los pares que pertenecen a la relación R (y = 2x) son solo:
R = {(2, 4), (3, 6), (4, 8)}
En esta relación vemos que: “4 es el doble de 2”; esto es, “4 es la imagen de 2 bajo R”, dicho de otro modo, “2 es preimagen de 4”.
Así, el dominio y rango son:
D = {2, 3, 4}
Rg = {4, 6, 8}
Según lo que vemos, ¿Qué relación hay entre el Dominio y el conjunto de partida?
En el Dominio falta el elemento 1 del conjunto de partida, por lo tanto el Dominio es un subconjunto de A.
Otra pregunta: ¿Todo elemento del conjunto de llegada es elemento del rango?
La respuesta es no, pues en el rango faltan el 5 y el 7.

Representación gráfica de las relaciones

Los pares ordenados se pueden representar gráficamente por medio de diagramas sagitales o por medio de puntos en el plano cartesiano . Veamos el siguiente ejemplo.
Ejemplo 4
Si  A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y  R la relación definida por la regla
R = {( x , y ) / y = 2 x + 1}, graficar  R.
Solución
Los pares ordenados que pertenecen  a la relación (que cumplen con y = 2x + 1) son:
R = {(1, 3), (2, 5), (3, 7), (4, 9)}
Y la gráfica correspondiente es la siguiente: